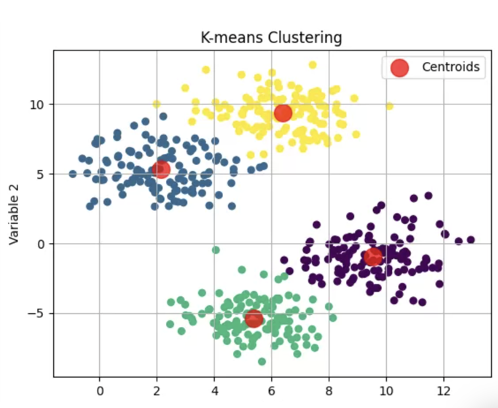
今回はクラスター分析についてまとめてみました。
データの行列を与えると、任意の数のクラスター(グループ)に分けてくれるので理解しやすく、使用頻度が高い解析方法ではないでしょうか。
クラスター分析の中で最も使われているk-means法を中心に、その内部理解ができるようまとめていきます。
いつものように主に下記の文献を参考にさせて頂きました。
機械学習のエッセンス -実装しながら学ぶPython,数学,アルゴリズム:加藤公一 著
amazonリンクはこちら
k-means法とは
データ分析をしていると、対象者をその属性や特徴でグループに分けたいという場面があると思います。そのような時に、与えられた各対象者のデータに基づき、自動的にグループ分けしてくれる分析方法です。
概要は以下です
- 被験者など各データの持ち主をグループ分けできる手法
- いくつのグループへ分けたいかは、分析者が決める必要がある
- グループごとの特徴はクラスター分析だけではわからないので、事後的に特徴量ごとの比較を行う必要はある
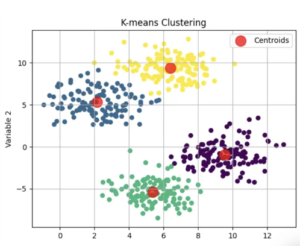
https://dalab.jp/mag/methods/cluster-analytics/
k-means法のアルゴリズム
k-means法では下記の式の解が最小となるようなクラスター割り付けを考えます。
\[
\sum_{i=1}^{k} \sum_{x \in C_i} \|x – \mu_i\|^2
\]
k : クラスター数
Ci:第iクラスター
x : データ点
μi:クラスターiの平均(重心)
上記の数式を文章にすると、
- 第iクラスターに属するデータ点全てについて、クラスター平均(重心という)との距離を計算(Aとする)
- Aの距離を全て合計し、各クラスターの合計距離(B)を計算 →
つまり3クラスター3つの、5クラスターなら5つの距離Bができます - 全てのクラスターのBを合算する(C)
ということです。この3行目で求めた合計距離Cを最小化する、つまり最もおさまりの良いクラスター分類を明らかにします。
初期設定〜クラスター決定までの流れ
まずは初期値としてのクラスター(重心)平均を任意に設定します。
各データに対し、下記の式が最小になるようなクラスターを割り当てます。
\[
\arg\min_{j} \|x_j – \mu_i\|
\]
つまりデータ数がjあるときに、j個全てのデータについて各クラスタの重心との距離を計算します。
そのうち、距離が最も小さいクラスターに割り振ります。
これを全データ分(j回)繰り返します。
j個のデータが割り振られたクラスターに基づき、各クラスターの重心を「更新」します。
値が収束するまで、上記のクラスター割り振り & 重心の更新作業を繰り返します。
プログラムでの実装
PythonやRでk-means法を実施する際の入出力は以下になります。
入力
RかPythonかで入力の方法は若干異なりますが、上記のアルゴリズムを理解できていれば問題ないかと思います。
基本、対象となるデータ、分けたいクラスター数は必須で、アルゴリズムを回す回数は任意に設定が可能になっていると思います。
- 目的変数の特徴量行列(例:購入頻度、年齢、性別など)
- 分けたいクラスター数
- 繰り返し回数の上限
from sklearn.cluster import KMeans
import numpy as np
X = np.array([[1, 2], [1, 4], [1, 0],
[10, 2], [10, 4], [10, 0]])
kmeans = KMeans(n_clusters=2, random_state=0, n_init="auto").fit(X)
kmeans.labels_
# array([1, 1, 1, 0, 0, 0], dtype=int32) これがクラスター割り当て結果
kmeans.predict([[0, 0], [12, 3]])
# array([1, 0], dtype=int32) 任意のデータ点を入れるとクラスター割り当て
kmeans.cluster_centers_
# array([[10., 2.],
[ 1., 2.]]) クラスターの重心(平均)