今回はロジスティック回帰についてまとめてみました。
SPSSやPython, Rによって実装は簡単になってきていますが、背景を理解するのはおっくうな方々も多いのではないでしょうか。文系出身者として、なるべくわかりやすくお伝えしたいと思います
結論として、
- ロジスティック回帰は
• 2値の目的変数(例:合格・不合格)を予測したい場合、あるデータフレーム(例:勉強時間、スポーツ歴 etc…)を入力すると、そのデータから目的変数を説明する確率を出力してくれます
• 確率0.5 (50%)を上回る方の目的変数を予測結果として出力します
• 出力される回帰係数に基づいてオッズ比を算出します
というものです。
今回も、「機械学習のエッセンス -実装しながら学ぶPython,数学,アルゴリズム」加藤 公一 著を参考にまとめました。読むのに少し気合のいる書籍ですが、このように丹念に読み込むと文系データ解析者のアルゴリズム理解力を飛躍的に伸ばしてくれそうな本です
書籍URL
ロジスティック回帰とは
目的変数が2値(0,1)の場合によく使われる分析方法で、各説明変数の回帰係数が大きいほど(1に近いほど)、目的変数を1に近づける力が強いというような解釈をします。
ではアルゴリズムについて理解を深めていきましょう。
d次元(d列)のデータフレームのある列の特徴量xについて考えます。目的変数y = 1となる確率をP( Y = 1 | X = x )とし、y = 0となる確率をP( Y = 0 | X = x )とすると、ロジスティック回帰の式は下記のようになります。
\[
P(Y = 1 \mid X = x) = \sigma\Big( w_0 + \sum_{j=1}^{d} x_j w_j \Big) = \sigma\big( w^T \tilde{x}^T \big) \tag{1}
\]
ここでσ(シグマ)は「シグモイド関数」です(この後まとめます)、w0は切片、xjはj列目の特徴量、wjは各説明変数に対応する回帰係数を指します。
つまり、右辺のシグモイド関数の入力には線形回帰と同じ式が入ります。
wのベクトルを斜文字wで表し、xの上に~(チルダ)がついているのはxベクトルの先頭に1を追加し、計算を楽にするための数学的な処理です。
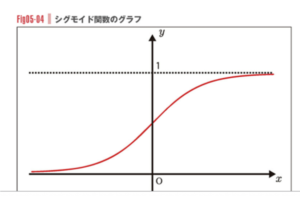
シグモイド関数とは
\[
\sigma(\xi) = \frac{1}{1 + e^{-\xi}}
\]
にょろっとしたギリシャ文字は「プサイ」といいます。eは指数です、また分母のe右肩の数値がマイナスになっているのは
\[ \frac{1}{1+\frac{1}{e^{\zeta}}} \]
と同じ意味です。つまりシグモイド関数は0 ~ 1の範囲に収まりつつ、入力値が大きいほど1に近づく性質を持つ関数です。
確率を最大化するようなw
数式(1)を踏まえると、あるデータフレームである特徴量xiのラベルがyになる確率を以下のように表すことができます。
\[
P\left(Y=y \,\middle|\, X=x\right)
= {P(Y=1 \mid X=x)}^y {P(Y=0 \mid X=x)}^{1-y}
= \sigma\left(\tilde{x}_k w\right)^y \left( 1 – \sigma\left(\tilde{x}_k w\right) \right)^{1-y}
\]
上記の式は、yもxも1つのみ(スカラー)の場合の式です。
実際のデータのように目的変数y, 説明変数xが2つ以上の数列(ベクトル)になる場合、
それぞれ掛け算をしていくため、
\[
P\left(y \mid X\right) = \prod_{k=1}^{n} \left[ \sigma\left(\tilde{x}_k w\right)^y \left( 1 – \sigma\left(\tilde{x}_k w\right) \right)^{1-y} \right] \tag{2}
\]
-logによる変形
数式(2)の確率を最大化するようなwを求めていきたいですが、掛け算の形に−logをかけること(L (w)とおきます)で計算可能な形に変換します。
\[
L(w) = -\log P(y \mid X)
= – \sum_{k=1}^{n} \Big[ y_k \log \sigma(\tilde{x}_k w) + (1 – y_k) \log (1 – \sigma(\tilde{x}_k w)) \Big]
\]
ul>
- ロジスティック回帰のアルゴリズムではここから難しくなってくるのですが、頑張って書いていきます。
目的は、上記の式L(w)の回帰係数wを求めることです。回帰係数がわかれば、確率計算まで持ち込めますので。まずL(w)を偏微分していくのですが、シグモイド関数の偏微分では以下の公式を利用できます。
シグモイド関数の微分
\[
\frac{d}{d\xi} \sigma(\xi) = \frac{d}{d\xi} \frac{1}{1 + e^{-\xi}}
\]
分数をマイナス累乗に変換して
\[
\frac{d}{d\xi} \sigma(\xi) = \frac{d}{d\xi} \frac{1}{1 + e^{-\xi}} = \frac{d}{d\xi} \left( 1 + e^{-\xi} \right)^{-1}
\]
合成関数の微分を使って
\[
\frac{d}{d\xi} \sigma(\xi)
= -1 \cdot \left( 1 + e^{-\xi} \right)^{-2} \cdot \frac{d}{d\xi} \left( 1 + e^{-\xi} \right)
= \frac{1}{\left( 1 + e^{-\xi} \right)^2} \cdot e^{-\xi}
= \frac{1}{1 + e^{-\xi}} \cdot \frac{e^{-\xi}}{1 + e^{-\xi}}
\]
シグモイド関数が出てきたので、
\[
= \sigma(\xi) \cdot \frac{(1 + e^{-\xi}) – 1}{1 + e^{-\xi}}
= \sigma(\xi) \left( 1 – \sigma(\xi) \right)
\]
となります。
L(w)の一階微分
確率式に- logをかけたL(w)を偏微分すると、
\[
\nabla L(w) = – \sum_{k=1}^{n} \Bigg[
y_k \frac{d}{dw} \log \sigma(\tilde{x}_k w)
+ (1 – y_k) \frac{d}{dw} \log \left( 1 – \sigma(\tilde{x}_k w) \right)
\Bigg]
\]
Log()の微分の公式 & 合成関数の微分を使って、
\[
\nabla L(w) = – \sum_{k=1}^{n} \Bigg[
y_k \frac{1}{\sigma(\tilde{x}_k w)} \frac{d}{dw} \sigma(\tilde{x}_k w)
+ (1 – y_k) \frac{1}{1 – \sigma(\tilde{x}_k w)} \frac{d}{dw} \big( 1 – \sigma(\tilde{x}_k w) \big)
\Bigg]
\]
先ほどまとめたシグモイド関数の微分と合成関数の微分を使って
\[
\nabla L(w) = – \sum_{k=1}^{n} \Bigg[
y_k \frac{1}{\sigma(\tilde{x}_k w)} \, \sigma(\tilde{x}_k w) \left( 1 – \sigma(\tilde{x}_k w) \right) \tilde{x}_k
+ (1 – y_k) \frac{1}{1 – \sigma(\tilde{x}_k w)} \, \left( – \sigma(\tilde{x}_k w) \left( 1 – \sigma(\tilde{x}_k w) \right) \right) \tilde{x}_k
\Bigg]
\]
分数部分を打ち消して、
\[
\nabla L(w) = – \sum_{k=1}^{n} \Big[
y_k \left( 1 – \sigma(\tilde{x}_k w) \right) \tilde{x}_k
– (1 – y_k) \sigma(\tilde{x}_k w) \tilde{x}_k
\Big]
\]
展開し、
\[
\nabla L(w) = – \sum_{k=1}^{n} \Big[
\big( y_k – \sigma(\tilde{x}_k w) \, y_k \big) \tilde{x}_k
– \big( \sigma(\tilde{x}_k w) – \sigma(\tilde{x}_k w) \, y_k \big) \tilde{x}_k
\Big]
\]
\[
\nabla L(w) = \sum_{k=1}^{n} \left[ \left( -y_k + \sigma(\tilde{x}_k w) \right) \tilde{x}_k \right] \tag{3}
\]
ここで 目的変数yはシグモイド関数のベクトル(確率のベクトル)になるので
\[
\tilde{y} = \sigma(\tilde{x}_k w_1), \, \sigma(\tilde{x}_k w_2), \dots, \sigma(\tilde{x}_k w_n)
\]
\[
\nabla L(w) = \tilde{X} \left( \tilde{y} – y_k \right)
\]
の形に単純化できます。
ここで▽L(w)は勾配なので、「ベクトル」です
ニュートン法
▽L(w)の回帰係数wを求めていく(最適化する)アルゴリズムにニュートン法があります。Pythonのscikit-learnのロジスティック回帰でもデフォルトのアルゴリズムはニュートン法です。
- ニュートン法とはある関数f(x) = 0となるようなxを求めたい時、f(x+1)の接線のy座標が0になるようなxを繰り返し求め、最終的な解に近づいていく…という方法です。

f(x)をf(x+1)を用いて表す便利な手法に「テイラー展開(接線の方程式)」があります。
\[
f(x) \approx f(x_t) + f'(x_t) (x_{t+1} – x_t)
\]
〜が2つ重なっているのは「近似」の記号です。
f(x) = 0とすると、
\[
0 \approx f(x_t) + f'(x_t)(x_{t+1} – x_t)
\quad \therefore \quad
x_{t+1} = x_t – \frac{f(x_t)}{f'(x_t)}
\]
となります。つまり1つ前の値xtから次のxt+1が求まるのですね。
2階微分(ヘッセ行列)
ニュートン法の式を今回のロジスティック回帰の式に置き換えると、
\[
w_{t+1} = w_t – \frac{\nabla L(w)}{H}
\]
ここでHは、▽L(w)をさらに偏微分したもので、ヘッセ行列といいます。
勾配はベクトルでしたが、勾配をさらに偏微分すると次元が1つ増え、行列になります。
ヘッセ行列を作成していきます。数式(3)より、
\[
\nabla L(w) = \sum_{k=1}^{n} \left[ \left( -y_k + \sigma(\tilde{x}_k w) \right) \tilde{x}_k \right]
\]
ヘッセ行列Hのi行j列の値は
\[
H_{ij} = \frac{d}{dw_j} \sum_{k=1}^{n} \left[ \left( \sigma(\tilde{x}_k w) – y_k \right) \tilde{x}_{ki} \right]
\]
シグモイド関数の微分の公式、合成関数の微分を利用して
\[
H_{ij} = \sum_{k=1}^{n} \left( \sigma(\tilde{x}_k w) \big( 1 – \sigma(\tilde{x}_k w) \big) \right) \tilde{x}_{ki} \, \tilde{x}_{kj}
\]
ここで シグモイド関数のベクトル(確率のベクトル)が目的変数yになるので
\[
\tilde{y} = \sigma(\tilde{x}_k w_1), \, \sigma(\tilde{x}_k w_2), \dots, \sigma(\tilde{x}_k w_n)
\]
\[
H_{ij} = \sum_{k=1}^{n} \tilde{y}_k \, (1 – \tilde{y}_k) \, \tilde{x}_{ki} \, \tilde{x}_{kj}
\]
とまとめることができます。
つまり目的変数と説明変数のベクトル積の形になりました。
ここでyk(1-yk)をk次元の対角行列Rと置くことで数式を単純化します。
\[
H = \tilde{X} R \, \tilde{X}
\]
- ※対角行列にベクトルをかけるとk行1列のベクトルになります。
 chatgptより
chatgptより
ここで先ほどのニュートン法へ戻ると
\[
w_{t+1} = w_t – \frac{\nabla L(w)}{H}
\]
より、
\[
w_{t+1} = w_t – \frac{\nabla L(w)}{\tilde{x}_{ki} \, R \, \tilde{x}_{kj}}
\]
\[
\nabla L(w) = \tilde{X} \left( \tilde{y} – y_k \right)
\]
よって、
\[
w_{t+1} = w_t – \frac{\tilde{X} \left( \tilde{y} – y_k \right)}{\tilde{x}_{ki} \, R \, \tilde{x}_{kj}}
\]
となり、現時点のwt+1を1つ前wtから求める式が完成しました。
Pythonコード
以上の理論を踏まえた上で、Python上でロジスティック回帰分析を行なってみます。coef、predictが回帰係数w、y = 1になる確率を示し、オッズ比の導出も簡単にできます。
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
iris_df = sns.load_dataset('iris') # データセットの読み込み
iris_df = iris_df[(iris_df['species']=='versicolor') | (iris_df['species']=='virginica')] # 簡単のため、2品種に絞る
X = iris_df[['petal_length', 'petal_width', 'sepal_length']] # 説明変数3列
Y = iris_df['species'].map({'versicolor': 0, 'virginica': 1}) # 目的変数_01変換後
X_train, X_test, Y_train, Y_test = train_test_split(
X, Y, test_size=0.2, random_state=0
)
lr = LogisticRegression()
lr.fit(X_train, Y_train)
lr.coef_# 回帰係数 w
#array([[ 2.8868383 , 1.98586881, -0.36119199]])
lr.predict(X_test) # 予測値Y
#array([0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0])
np.exp(lr.coef_) # オッズ比(exp * 回帰係数)
array([[17.93651003, 7.28537423, 0.6968452 ]])

