データ分析や機械学習の関連で、線形回帰・リッジ回帰・ラッソ回帰という言葉をよく聞きます。線形回帰とリッジ・ラッソ回帰の違いは何なの?それぞれのメリット・デメリットを知りたいという自分の疑問に答えるため、まとめてみました。
今回も「加藤公一:機械学習のエッセンス 実装しながら学ぶPython、数学、アルゴリズム」を参考にまとめさせていただきました。

ラッソ回帰とは
リッジ回帰では、L2正則化を用いて、回帰係数(w)が外れ値などにより大きな変化を起こすことを防いでいました。ラッソ回帰では回帰係数に「スパース性」を持たせることが特徴です。
つまり、多変量解析で、関係のない回帰係数は0に。本当に関係のある回帰係数だけは0以上にします。そうすることで回帰分析の出力の解釈可能性を向上させます。
ラッソ回帰では、L1正則化を用います。
左辺の記号はファイと読みます。
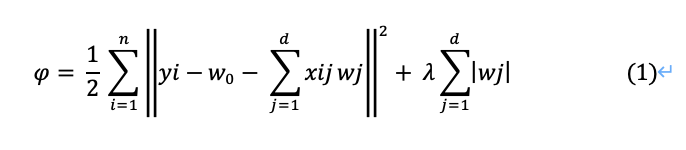
右辺の第2項がL1正則化を加えている部分です。
つまり第1項は残差(予測誤差)を示しています。また第2項は正則化による回帰係数へのペナルティを示しています。ここでj は1以上なので、切片w0はペナルティに含まれません。
L1正則化とL2正則化の違い
数学的な詳細を省き直感的に説明をすると、
– L2正則化(リッジ回帰:2乗する方)は回帰係数を小さくするが0にはしない
– L1正則化(ラッソ回帰)は小さい回帰係数は0にする→無駄な説明変数を除外する機能
というところでしょうか
微分不可能
このラッソ回帰の式(1)は「微分不可能」と言われています。「微分不可能」とは何でしょうか?
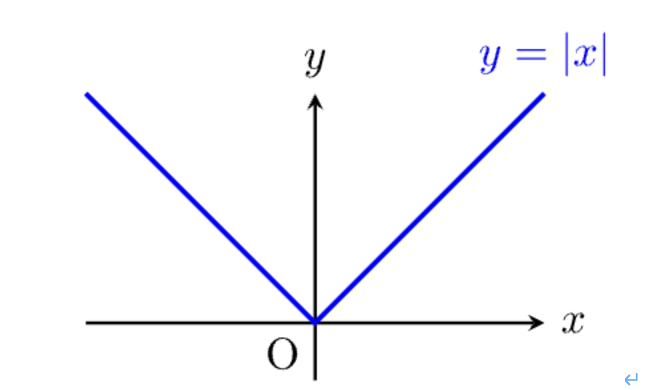
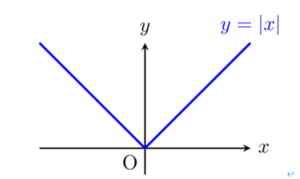
下記の図のように、原点を境に2つの異なる関数になってしまう場合、「微分不可能」といいます。言い換えると、以下のようにも言えます。
– 左側(左微分)と右側(右微分)が重ならない
– 連続性がない
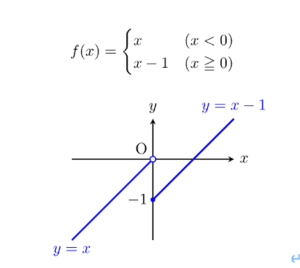
参考:https://yama-taku.science/mathematics/one-step-math/non-differentiable/
ここで、ラッソ回帰の式に含まれるL1正則化の部分も微分不可能となります(左微分と右微分が一致しない)
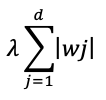
下図のように、左微分の傾きと右微分の傾きが一致せず左右対称になっている、つまり微分不可能であることがわかります。
回帰係数wの導出
前述の通り、ラッソ回帰では微分不可能なので左微分と右微分に分けて式を立てます。
ラッソ回帰の式は
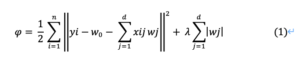
だったので、この左辺ファイをwk (kは0以外)で偏微分していきます。
合成関数の微分を利用して、右微分は
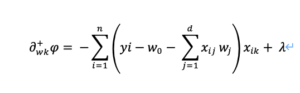
左微分は、λの符号が逆になり、
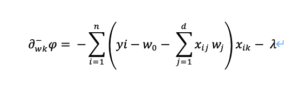
右微分を0と置くと、先頭のマイナスをλの前に移行して、
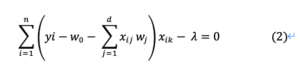
上式(2)をwk (kは0以外) について解くと、式のwjの中にwkも含まれているため区別して示すと、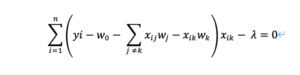
左辺の第3項を分離してxikでまとめると
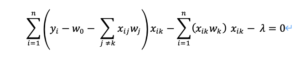
ここからwkを求めていきます
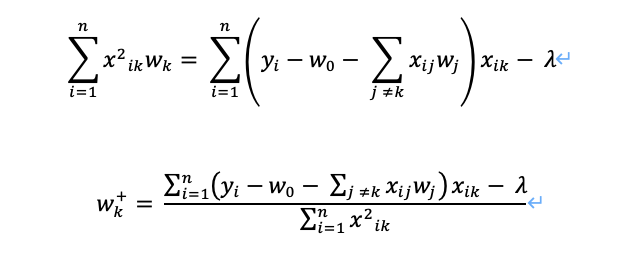
同様の解法で、左微分のwkも求めると、右微分とはλの符号が逆になり
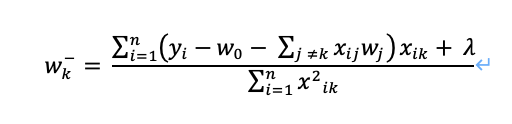
ソフトしきい値
ここで、「ソフトしきい値」という概念を使います。そもそもラッソ回帰は「スパース性」を持たせることがその本質でしたが、この「ソフトしきい値」によってこの目的を達成します。注意:ソフトマックス関数とは別のものです
ソフトしきい値は下記で表せます。
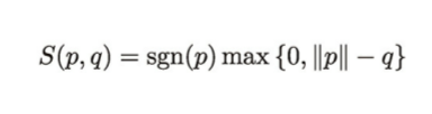
ここでsgn()は符号関数というもので、下記のように表します。
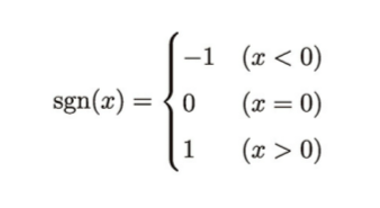
つまり、S()に2つの引数(p,q)を代入すると、まず符号はsgn()が0以上か否かで決定されます。ついで、max()の部分で0か2つの引数の差分の大きい方を取得します。
ソフトしきい値の適用
Wkを更新していく式にソフトしきい値を当てはめます。
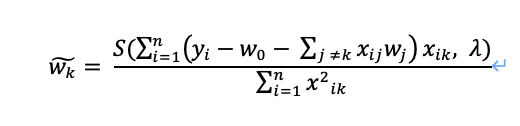
つまり、以下の条件が適応されます。

この処理によって、ラッソ回帰の「スパース性」という性質が担保されています。
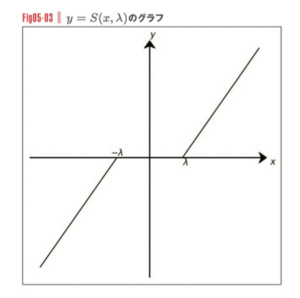
加藤公一:機械学習のエッセンス 実装しながら学ぶPython、数学、アルゴリズムより
ここではyが回帰係数を示します。-λ ~ λの範囲内はy = 0になっているのがラッソ回帰の特徴を表しています。
まとめ
多変量解析の際に、ラッソ回帰では±λの範囲内に回帰係数が収まる説明変数では、その回帰係数を0にリセットします。これがラッソ回帰のスパース性です。
実際にpythonやRでラッソ回帰を行う際は、ハイパーパラメータとしてλを設定しますが、λが大きいほど強いスパース性を持つので、本当に関係のある回帰係数だけを取得することが可能になります。