【R】Rでのχ二乗検定の方法です【データの尺度についておさえましょう】

✅疑問
・Rでχ二乗検定を行う方法がわからない

・２つの群の比較をしたいけどどの方法を取ればいいの？

こういった疑問に答えます

Rでのχ二乗検定はネットで調べてもすぐに解決策が出てこず、わかりづらいのでまとめてみました。
また、特に統計初心者や学生の卒業論文の際は統計手法の選択に迷うことがあるのではないでしょうか。

本記事を読めば、

・状況に応じた統計手法の選択が可能になります。

・Rを使ったクロス集計表の作成、χ二乗検定が出来るようになります。

本記事ではまず統計手法の選択をどのように行うのか紹介し、次にRでのχ二乗検定の方法を説明します。

■ 4つのデータ尺度を知りましょう　～検定方法の選択に重要です～
■比較する尺度ごとに統計手法をまとめてみました
■ Rでのχ二乗検定の方法を紹介します。

■ 4つのデータ尺度を知りましょう　～検定方法の選択に重要です～

世の中には様々なデータがありますよね。例えばA型の人の人数やある商品を購買した人の平均年齢、サッカーの試合で左サイドから打ったシュートの数などです。
このような無数にあるデータの種類は4つの尺度で分類でき、その尺度ごとに統計手法が変化します。
では一つずつ解説していきます。

①名義尺度

名義尺度はその名の通り名称です。例えば性別、血液型、郵便番号、出身地などです。

②順序尺度

順序尺度は「順位をつける」ような尺度です。順位や大小には意味がありますがその間隔には意味がないもの。足し算や引き算ができないもの。
例えば「1位2位3位」や「1好き2普通3嫌い」などです。
「1好き+2普通＝3嫌い」という関係は成り立たないですよね。

③間隔尺度

「目盛りが等間隔になっているもの」です。また、「0」でも存在があるものです。「０」でも存在があるとはどういうことでしょうか。例えば温度や西暦は0度や0年でも存在しますよね。0が任意に決まっているからです。

④比例尺度

間隔尺度と異なり「0が存在しないもの」です。但し間隔尺度と同様、目盛りは等間隔です。
例えば身長、速度、値段、睡眠時間などです。
間隔尺度と比例尺度は区別しないで扱うことが多いです。

■比較する尺度ごとに統計手法をまとめてみました

たくさんある統計手法の中でどれを使用すればいいのか、選択する時に困りますよね。データがどの尺度に当たるのかによって方法が大体決められるのでまとめてみました。

説明変数（独立変数）		2群	3群以上
	名義尺度	χ二乗検定	χ二乗検定
	順序尺度	ウィルコクソンの検定（順位和、符号付順位）	クラスカルウォリスフリードマン
	間隔or比率尺度	ｔ検定	一元配置分散分析二元配置分散分析 ※ただしノンパラメトリック検定を用いる場合もあり

説明変数とはそれぞれの群に属するデータくらいの理解でひとまず大丈夫です。
表の見方ですが、
名義尺度は2群でも3群以上でもχ二乗検定を用います。
順序尺度はノンパラメトリック検定を用います。なので2群ではウィルコクソンの検定を、3群以上ではクラスカルウォリス検定やフリードマン検定を用います。
間隔・比例尺度では2群ではt検定、3群以上では一元配置分散分析か二元配置分散分析を用います。（正規性の検定の結果、ノンパラメトリック検定になることもあります。）

2群の場合と3群以上の場合で検定方法は異なり、正規性の有無も検定方法に影響します。
正規性の有無に関してはRでの正規性の検定　【正規性をまず検定しましょう】をご参照ください。

■ Rでのχ二乗検定の方法を紹介します。

本日はRを使ったχ二乗検定の方法を紹介します。
以前の記事でRを使ったt検定やウィルコクソンの検定（順位和、符号付順位）は紹介しました。興味ある方はこちらご参照ください。
Rによる2群間検定　【4種類解説しました】

今回は、2群以上の名義尺度を比較するχ二乗検定の方法を紹介します。
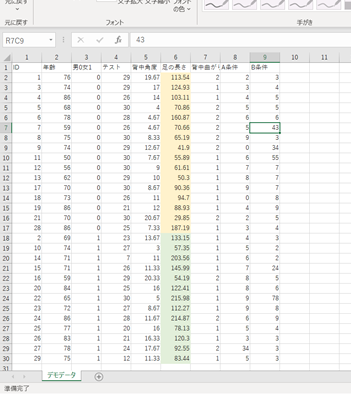
CSVファイルにまとめたデモデータを使用します。
デモデータはこちら

↑7行目の背中曲がりの有無（0:なし1:あり）を性別(0:男性 1:女性)で比較してみます。
性別と背中曲がりはどちらも「なし、あり」で表されるので名義尺度です。
なのでχ二乗検定を使用します。

※ちなみに5行目の背中角度や6行目の足の長さを性別で比較する場合は、それぞれ比率尺度か間隔尺度になるのでt検定もしくはウィルコクソンの検定を用います。

帰無仮説は「性別によって背中曲がりの有無に差はない」です。
ではRでこのCSVデータを読み込んでみましょう。
読み込み方法の詳細がわからない方はこちらの記事をご覧ください。
Rにexcelで作ったファイルを読み込む方法【CSV形式で読み込みましょう】

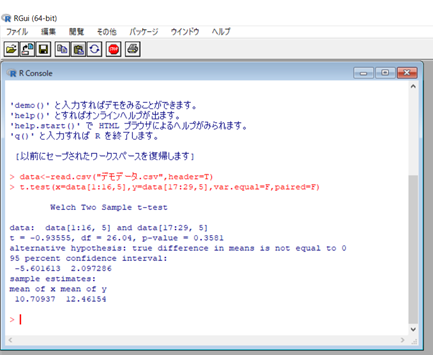
read.csv　関数で読み込んで、data という名前で保存します。

data<-read.csv(“デモデータ.csv”,header=T)

χ二乗検定を行った結果がこちらになります。

↑説明していきますね。
　Rでχ二乗検定を行う際は、二段階になっています。
まず、table関数を用いてクロス集計表を作成します。

table (データ7行目 , データ3行目)

↑と書くことで、2行×2列のクロス集計が書けます。
上の0,1行が背中曲がり[0:なし,1:あり]（7行目）、下の0,1列が性別[0:男性,1:女性]（データ3行目）です。
背中曲がりなしの男性6名、女性10名で背中曲がりありの男性が5名、女性8名ですね。
上手くクロス集計表が出たら、xという名前でクロス集計データを格納します。

ここまで来たら、χ二乗検定を行います。

χ二乗検定の関数は

chisq.test(対象のデータ名)