今回はサポートベクトルマシンのカーネル関数版についてまとめてみました。(前回は線形分離可能なバージョンのアルゴリズムを紹介しました。)サポートベクトルマシン(前編:線形分離可能)
まとめ
・カーネル関数の線形バージョンを少し変形したものが、カーネル関数の使用バージョンである
・SVMのコアは線形でもカーネル関数を用いた非線形でも、ラグンジュ乗数αを求めることにある
・ただしαを求めるアルゴリズムは難しい
・数式はざっくり、流れを理解することに重点を置いた
カーネル関数とは何でしょうか?ますはそこから理解を深めていきたいと思います。
カーネル関数とは
機械学習の界隈ではよく耳にする言葉ですが、意味をあまり理解していないで使っている方も多いのではないでしょうか?(私も最初はあまり…)
低次元のデータを線形分離では分類しきれない場合に、高次元へ変換(写像といいます)して分類できるようにする関数
イメージとしては、1次元の数式では直線が引けますが円や曲線は描けませんよね。これを2次以上の式へ変換することによって円や曲線を描けるようにします。
参照先:
https://www.shuei-yobiko.co.jp/labo/jh-math-byousatsu09/
https://univ-juken.com/en-hoteishik
https://kenyu-life.com/2019/04/12/non_linear_svm_parameter_identification/
サポートベクトルマシン(SVM)の簡単なおさらい
サポートベクトルマシン(SVM)について
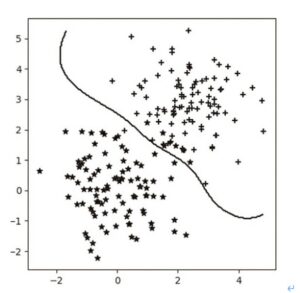
サポートベクトルマシンはデータを分類するような直線(前回取り上げた)や曲線(今回まとめる)を引くことによって、データから結果を予測できるような機械学習の手法でした。
SVMの重要な概念として「マージン最大化」があります。つまりデータを分類する線から、最も近い位置にある点までの距離を最大化するというものです。
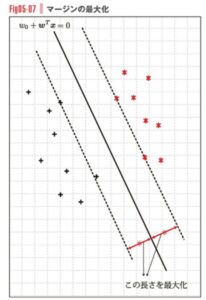
Screenshot
加藤 公一:機械学習のエッセンスより
マージン最大化とラグンジュ未定乗数
分類線の係数をwとするとき、αはw,x,yから派生したダミーの変数です(ダミー変数を追加することにより、本来求めたいwを効率的に求める手段がラグンジュ未定乗数というイメージです)
線形分離するSVMではマージンを最大化する式を変形した下記の式を、その制約条件(例えば、α > 0のように各変数固有の条件を与えること)に合うように最適化してαを求めていました。
\( -\frac{1}{2} \sum_{i=1}^{n} \sum_{k=1}^{n}
\alpha_i y_i \alpha_k y_k \, x_i^{T} x_k
+ \sum_{k=1}^{n} \alpha_k \)
カーネル関数を適応するもほぼ同様で、xの部分を下記のようなカーネル関数へ変換するだけです。
\(\phi(x)\)
\[
\text{Maximize}\quad
f(\alpha)=
-\frac{1}{2}
\sum_{i=1}^{n}\sum_{k=1}^{n}
\alpha_i y_i \alpha_k y_k
\; \phi(x_k)^{T} \phi(x_i)
+\sum_{k=1}^{n}\alpha_k
\tag{1}
\]
\[
\text{subject to }\quad
\sum_{i=1}^{n} \alpha_i y_i = 0
\]
\[
0 \le \alpha_i \le C
\]
となります。Subject toは制約条件を示す記号です。
この式(1)は何を示しているかというと、
・分類線(サポートベクトル)と近接点の距離の最大化式
\[
\max_{w_0,\, w}\;
\frac{1}{\|w\|}
\min_{i}\; y_i \left( w_0 + w^{T}\phi(x_i) \right)
\]
\[
\text{subject to }\;
y_i \left( w_0 + w^{T}\phi(x_i) \right) = 1
\]
このsubject toが1なのは分類線の直上に点が位置している想定
この式を合わせこみ、ラグンジュ未定乗数で新しい変数αで置き換えたものが数式(1)になります。
数式(1)のαを求めることで、wも求めることができ、分類線の座標が明らかになる(つまり線が引ける)わけです。
また、カーネル関数は
\[
K(x_k, x_i) = \phi(x_k)^{T} \phi(x_i)
\]
とまとめることができます。
先ほど書いた通り、この数式(1)からαを求めることがゴールです。
・インデックスiとjを同時に更新していき、制約条件を満たす最適なαを探す(詳細は成書をご参照ください)
変数αを求めると何が起こるか
上記のように逐次i, jを更新しαを求めることで、何が起こるのでしょうか。
前回の線形版でも同様でしたが、このαはラグンジュ乗数というもので、ラグンジュの未定乗数を使うために生まれてきたいわばダミーの変数です。アルファだけではまだサポートベクトルを描画できません。
最近接点からの距離が0になるような、wを求める下記の式があります。
この数式にαを代入し、w行列を求め、非線形な境界線がひけるわけです。
\[
w^{T}\phi(x) = \sum_{i=1}^{n} \alpha_i y_i K(x_k, x_i)
\]
Screenshot
カーネル関数版のSVMをpythonで実装
pythonではsklearnライブラリを使用します
重要なパラメータとしては、以下がある
・kernel:使用するカーネル関数を決める
・C:正則化パラメータ(誤りの分類をどこまで許容するかを決定するパラメータ) Cは最小距離を求める数式に加算され、Cが大きいほど微小な誤りに厳しくなり過学習傾向になる
・gamma:カーネル関数の広がりを規定。大きいほど細かな分類境界、小さいほど大雑把な境界になる
・degree:多項式の次数 ・coef0:多項式の定数項(デフォルト=0) ・max_iter:最大繰り返し回数(デフォルト=-1 (無制限))
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score, classification_report
from sklearn.preprocessing import StandardScaler
import numpy as np
# -------------------------
# 1. データ読み込み
# -------------------------
iris = datasets.load_iris()
X = iris.data # 特徴量
print(X)
y = iris.target # クラスラベル
print(y)
# 2クラス分類にする場合(0と1だけ使う)
# コメントアウト解除すると二値分類になる
# X = X[y != 2]
# y = y[y != 2]
# -------------------------
# 2. Train / Test 分割
# -------------------------
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=42
)
X_train.size
X_test.size
# -------------------------
# 3. 標準化
# -------------------------
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# -------------------------
# 4. カーネルSVMモデル(RBF)
# -------------------------
model = SVC(
kernel='rbf', # カーネル関数
C=1.0, # 正則化パラメータ
gamma='scale' # カーネルの広がり
)
# -------------------------
# 5. 学習
# -------------------------
model.fit(X_train, y_train)
# -------------------------
# 6. 予測
# -------------------------
y_pred = model.predict(X_test)
# -------------------------
# 7. 精度評価
# -------------------------
acc = accuracy_score(y_test, y_pred)
print(f"Accuracy: {acc:.4f}")
print("\n--- Classification Report ---")
print(classification_report(y_test, y_pred))


