サポートベクトルマシン（前編：線形分離可能）

R
Screenshot

今回はサポートベクトルマシンについてまとめてみました。
SPSSやPython, Rによって実装はできるようにはなってきていますが、特に私のように文系出身者にとっては、背景を理解するのはこれまでまとめた回帰分析以上に難解に感じる方々も多いのではないでしょうか。頑張ってアルゴリズムのまとめにつとめます。

今回も、機械学習のエッセンス　加藤公一　著を参照させて頂きました。リンク

 

結論として、

サポートベクトルマシンは
• 多変量のデータを２つのグループに分類する手法
• 境界線を引くことによってグループを分離する
• 線形分離可能なパターンと、非線形での分離のパターンがある
• アルゴリズムが複雑なため、計算量は多いらしい
というものです。

今回は、まず線形分離可能なパターンをまとめ、次回に非線形のパターンに入っていきたいと思います。

サポートベクトルマシンとは

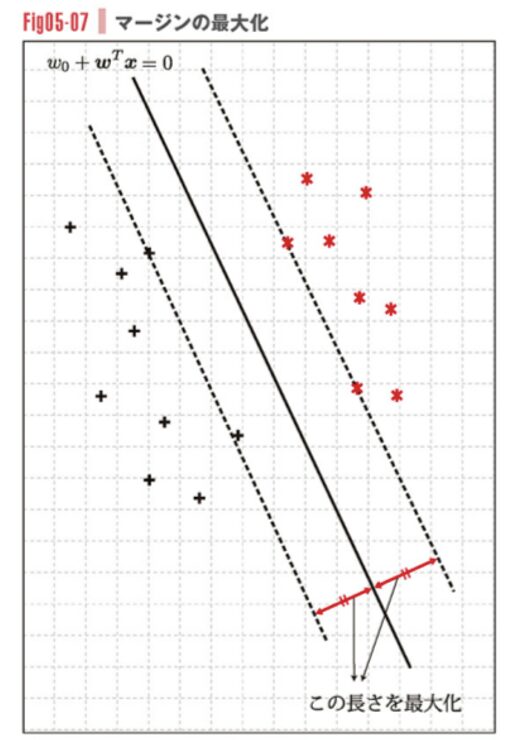
下記の散布図のイメージのように、「２つの集団へ分類する」ときに使用します。先日まとめたロジスティック回帰に使用目的は似ているかと思います。

サポートベクトルマシンでは集団を分離する境界線と、最も近い距離にある点を特定します。
この境界線と最も近い点の距離をマージンと言い、マージンを最大化させるには境界線をどこへ引くかを考えます。

マージンを最大化させる境界線を引くことで、データを分類する方法です

Screenshot

なお、説明変数が多変量になってくるので次元数は3,4,5…と増えていき、分離する直線（曲線）は超平面（超曲面）になっていきます。

境界線（面）の数式

この境界線（面）を表す式は下記のようになります

\( y = w_0 + \sum_{i=1}^{n} w_i x_i = w_0 + w^T x \)

w0は切片、wTxのwは回帰係数、xは個々の説明変数（特徴量）になります。
あるデータxがあったときに、回帰係数wをそこにかけることでy座標がもとまり、境界線が作られていくイメージです。
目的変数yは分類結果であり、ー1または1として考えていきます。

全ての点が完全に正しく分類できた時を考えると、

\( y\left(w_0 + w^T x\right) > 0\)

となり、あるi番目のデータxから境界線の距離は以下のように表されます

\[
\frac{y (w_0 + w^{\mathrm{T}} x_i)}{\|w\|}
\]

この境界線からの距離を最大化することを考えるので、
数式にすると、

\[
\max_{w_0,\,w}\ \min_i\ \frac{y_i\,(w_0 + w^T x_i)}{\|w\|}
\]

意味としては、内側のminで境界線の距離が最も小さいi番目のデータxを求めつつ、外側のmaximizeでは、切片w0と回帰係数wを動かしつつその距離を最大化する場所を探索するようなものです。

分母のwは外に出すことができ、
\[
\max_{w_0,\,w}\ \frac{1}{\|w\|}\ \min_i\ y_i\,(w_0 + w^T x_i)
\]
となります。

ここではうまく分類できた場合を考えているため、内側のmin y(w0 + wTxi)は1より大きいと考えます。またここでの境界線は線形のため、min y(w0 + wTxi)を1に置き換えることができます。

以下のようなイメージです

・min y(w0 + wTxi) = 1：境界線の直上に最も近い点（データx）が存在する
・mini y(w0 + wTxi) > 1：分類は成功し、境界線から少し離れて最も近い点（データx）が位置

従って、以下の最適化の式に集約できます

\begin{aligned}
& \max_{w_0,\,w} \frac{1}{\|w\|} \\
& \text{subject to} \quad y_i \left( w_0 + w^T x_i \right) = 1
\end{aligned}

ここでの、subject toとは、「ただし以下の条件で..」という意味です。「制約条件」と言います。
「y(w0 + wTxi) = 1」は、最も近い点が境界線の直上に位置していることを意味します。

1 / ||w||を最大化するwを求めることがここでのゴールですが、 それは||w||を最小化する問題に置き換えることができます。また、今後の計算のしやすさのために、1/2をかけ、２乗して以下のように変形します。

\begin{aligned}
& \min_{w_0,\,w} \frac{1}{2} \|w\|^2 \\
& \text{subject to} \quad y_i \left( w_0 + w^T x_i \right) = 1
\end{aligned}

ラグンジュの未定乗数法

上記のように２次式以上の次数の最適化(最も大きなor 小さな 値を求める)で、制約条件付きの場合はラグンジュの未定乗数法を使います。名前を聞いただけでギブアップしそうなところですが、グッとこらえてみます。

ラグンジュの未定乗数法は上記のような最適化したい式と、制約条件の式を合体させた１つの関数を作り、最適化したい変数を求めるという取り組みになっています。

ということでまずは、上記の２つの式をまとめていきたいのですが、今回はxiのiはn個あるパラメータの１つなので
\[
a = \left(a_1, a_2, \cdots, a_n \right)^T
\]
という変数を設定し、以下のようなL関数に１つにまとめます。

このαのような、式を合体させる際に付属する変数をラグンジュ乗数といい、Pythonのサポートベクトルマシンでも出力される数値になります。
以下の式でのw, w0の最適値を求めていきます。
先ほどのwに関する式と、制約条件が１つの数式にまとまっているのがわかります

\[
L\left(w_0, w, \alpha\right) = \frac{1}{2} \|w\|^2 – \sum_{i=1}^{n} \alpha_i \left\{ y_i \left( w_0 + w^T x_i \right) – 1 \right\} \quad (1)
\]

w0とwについての偏微分が0になることが極値を求めるステップですので、

\begin{aligned}
\frac{\partial}{\partial w_0} L\left(w_0, w, \alpha\right) &= -\sum_{i=1}^{n} \alpha_i y_i = 0 \\
\frac{\partial}{\partial w_j} L\left(w_0, w, \alpha\right) &= w_j – \sum_{i=1}^{n} \alpha_i y_i x_{ij} = 0
\end{aligned}

従って、

\begin{aligned}
\sum_{i=1}^{n} \alpha_i y_i &= 0 \quad (2) \\
w_j &= \sum_{i=1}^{n} \alpha_i y_i x_{ij}, \quad j = 1, 2, \dots, d \quad (3)
\end{aligned}

カルーシュ・クーン・タッカー条件（KKT条件）

ここで、ラグンジュの未定乗数ではさらに、以下の条件に従うことがわかっています。これをカルーシュ・クーン・タッカー条件（KKT条件）と言います。
様々な条件付けをすることによって、方程式の解を局所的なものに安定させているのですね。

\begin{aligned}
\alpha_i &> 0 \\
y_i \left( w_0 + w^T x_i \right) – 1 &\ge 0 \\
\alpha_i \left\{ y_i \left( w_0 + w^T x_i \right) – 1 \right\} &= 0
\end{aligned}

最適化の式の展開

さて、元々求めたいのは

\[
L\left(w_0, w, \alpha\right)
= \frac{1}{2} \|w\|^2
– \sum_{i=1}^{n} \alpha_i
\left\{ y_i \left( w_0 + w^T x_i \right) – 1 \right\}
\quad (1)
\]

でのwでした。
右辺の第１項を展開して各特徴量の回帰係数の２乗の和の形にし、
\[
\frac{1}{2} \|w\|^2 = \frac{1}{2} \sum_{j=1}^{d} w_j^2
\]

数式(3)を代入し、
\[
\begin{aligned}
=~& \frac{1}{2}\sum_{j=1}^{d}\left(\sum_{i=1}^{n}{\alpha_i y_i x_{ij}}\right)^2 \\
=~& \frac{1}{2}\sum_{j=1}^{d}\left(\sum_{i=1}^{n}{\alpha_i y_i x_{ij}}\right)\left(\sum_{k=1}^{n}{\alpha_k y_k x_{kj}}\right) \\
=~& \frac{1}{2}\sum_{i=1}^{n}\sum_{k=1}^{n}{\alpha_i y_i x_i \alpha_k y_k x_k}
\end{aligned}
\]

そして、右辺の第２項を展開、数式(3)を代入し、
\[
\begin{aligned}
& -\sum_{i=1}^{n}{\alpha_i\left\{y_i\left(w_0 + w^T x_i\right) – 1\right\}} \\
=~& -\sum_{k=1}^{n}{\alpha_k\left\{y_k\left(w_0 + \sum_{i=1}^{n}{\alpha_i y_i \sum_{j=1}^{n} x_{ij}} x_i\right) – 1\right\}} \\
=~& -w_0\sum_{k=1}^{n}{\alpha_k y_k} – \sum_{k=1}^{n}\sum_{i=1}^{n}{\alpha_k y_k \alpha_i y_i x_i^T x_k} + \sum_{k=1}^{n}{\alpha_k}
\end{aligned}
\]

式(2)を代入し、
\[
= -\sum_{k=1}^{n}\sum_{i=1}^{n}{\alpha_k y_k \alpha_i y_i x_i^T x_k} + \sum_{k=1}^{n}{\alpha_k}
\]

従って、
\[
\begin{aligned}
L\left(w_0,\, w,\, \alpha\right)
&= \frac{1}{2}\sum_{i=1}^{n}\sum_{k=1}^{n}{\alpha_i y_i \alpha_k y_k x_i^T x_k}
– \sum_{k=1}^{n}\sum_{i=1}^{n}{\alpha_k y_k \alpha_i y_i x_i^T x_k}
+ \sum_{k=1}^{n}{\alpha_k} \\
&= -\frac{1}{2}\sum_{i=1}^{n}\sum_{k=1}^{n}{\alpha_i y_i \alpha_k y_k x_i^T x_k}
+ \sum_{k=1}^{n}{\alpha_k}
\end{aligned}
\]
のように、wは消え、aだけについての最適化問題になりました。

2次計画問題

ここまでくると、次の目的はラグンジュ乗数aを求めることです。αを求めることで、データxの回帰係数wを求めることができ、（wは下記の式で求まるからです）、最適な境界線が明らかになってきます。

\[
w_j = \sum_{i=1}^{n} \alpha_i y_i x_{ij}
\]

このαを求める段階を2次計画問題と言います。2次計画問題とは、2次式についてある条件を守りつつ最適化（最大・最小値を求める）ことです。つまり、

\[
\begin{aligned}
& \text{Maximize} && f(\alpha) = \sum_{k=1}^{n} \alpha_k – \frac{1}{2} \sum_{i=1}^{n} \sum_{k=1}^{n} \alpha_i y_i \alpha_k y_k \, x_i^T x_k \\
& \text{Subject to} && \sum_{i=1}^{n} \alpha_i y_i = 0, \\
& && \alpha_i \ge 0, \\
& && \alpha_i y_i w_0 + w^T x_i – 1 = 0.
\end{aligned}
\]

を満たすようなαを求める問題になります。

2次計画法の詳細については、この記事では割愛させて頂きます。

この記事では、サポートベクトルマシンでは、分類直線を決定する必要がありますが、その境界線を決めるためにもラグンジュ乗数α、回帰係数w、切片w0を求める必要がある。そしてその求め方の概要を説明した。そのあたりでいったんのゴールとさせてください。

分類結果の出力

さて、分類曲線を引くのに必要なwが求まりました。ここで最初の議論に立ち返ると、

\[
y_i \left( w_0 + w^T x_i \right) > 0
\]

が正しく分類をされる指標でした。
分類結果とはつまりy（目的変数）であるので

\[
y = \operatorname{sign}(w^T x + w_0)
\]

で求められます。signとは入力値が0以上なら1を0未満なら-1をかえす関数です。
Pythonではこの-1を0に変換して出力しています。

Pythonコード

# ライブラリをインポート
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.datasets import make_classification

# データを生成 (2次元データ, 2クラス)
X, y = make_classification(
    n_samples=100,  # サンプル数
    n_features=2,   # 特徴量数
    n_informative=2,
    n_redundant=0,
    n_clusters_per_class=1,
    class_sep=0.8,
    random_state=1000
)
X.shape # 100,2　説明変数（特徴量）
y.shape # 100　ベクトル　正解ラベル

# 線形SVMモデルを作成
model = SVC(kernel='linear') # linearなので線形分離
model.fit(X, y)

model.coef_# 回帰係数wを特徴量の数出力
# array([[-1.29916954,  1.73173656]]) # 特徴量ごとの回帰係数

model.intercept_ # 切片w0
#array([0.96513541])

model.dual_coef_ # ラグンジュ乗数α
# array([[-0.72005683, -1.        , -0.42503852, -1.        , -1.        ,
#         -1.        , -1.        , -1.        , -1.        ,  1.        ,
#          1.        ,  1.        ,  1.        ,  1.        ,  1.        ,
#          1.        ,  0.14509535,  1.        ]])
model.support_vectors_# 境界線上に位置する座標点
# array([[ 0.060381  , -1.08911704],
#        [ 0.12434517, -0.82347453],
#        [ 0.84693998, -0.49957363],...
model.predict([[0.1,0.1]]) # 新しい点を与えてみる
# array([1])　予測結果
タイトルとURLをコピーしました