2022.2.26リライトしました。
二限配置分散分析ってどういう仕組みなんだろう。
主効果とか、交互作用とかわかりにくい。。
本日はこのような疑問にお答えします。
私は医療系大学院に通い、５年目。これまでにSPSSやRを使ってデータ解析、学会発表、論文発表を行えています。そのような僕が今回は二限配置分散分析をその理屈から、実装までをわかりやすく説明していきますね。
一元配置分散分析と二元配置分散分析の違い
前回の記事で一元配置分散分析について解説しました。
↑
一元配置分散分析も知りたい方はこちらどうぞ。【文系でも10分で理解できる】一元配置分散分析の原理、計算手順とは？
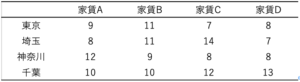
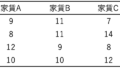
↑こんな感じの３群以上の比較のために、一元配置分散分析は用いたのでした。この図は、各都道府県の架空の平均家賃を表したもので、東京、埼玉、神奈川、千葉の平均家賃を比較できますね。
一元配置分散分析の特徴：
・データ全体(16個)の平均値
・各条件（都道府県）の平均値
を求め、計算に進んでいくのでした。
二元配置分散分析の特徴
一方の二元配置分散分析ではこんな感じのデータを扱います。
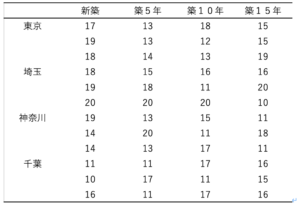
単位：平均家賃（円）です。
実は違う点があります。
先ほどの一元配置分散分析とは何が違うんでしょうか？
データの列部分を見てもらうと、「築年数による分類」がされていますよね。一元配置分散分析では、築年数まではカバーしていません。
つまり、二元配置分散分析を使うことにより、家賃の比較を、都道府県×築年数という二軸での比較を行うことができるのです。
では二元配置分散分析の具体的なステップに入っていきますね。
二元配置分散分析のstep by step
二限配置分散分析のポイントは以下です。一元配置と似ています。
二元配置分散分析は下の分散分析表を埋め、F値を求めていくことがポイントです。（ここは一元配置分析と同じです）
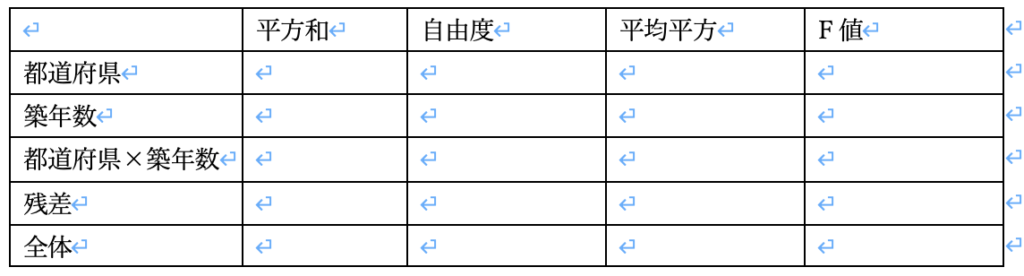
今回の解析対象データ（都道府県と家賃、築年数の表）
都道府県ごとに無作為に賃貸住宅を選び、家賃を並べた表を以下に載せます。
↓
step1 いろいろな平均値と平方和を求める
まず色々な平均値を求めなくてはなりません。
以下のように4種類の平均値を求めます。
一つずつ説明を加えますね。
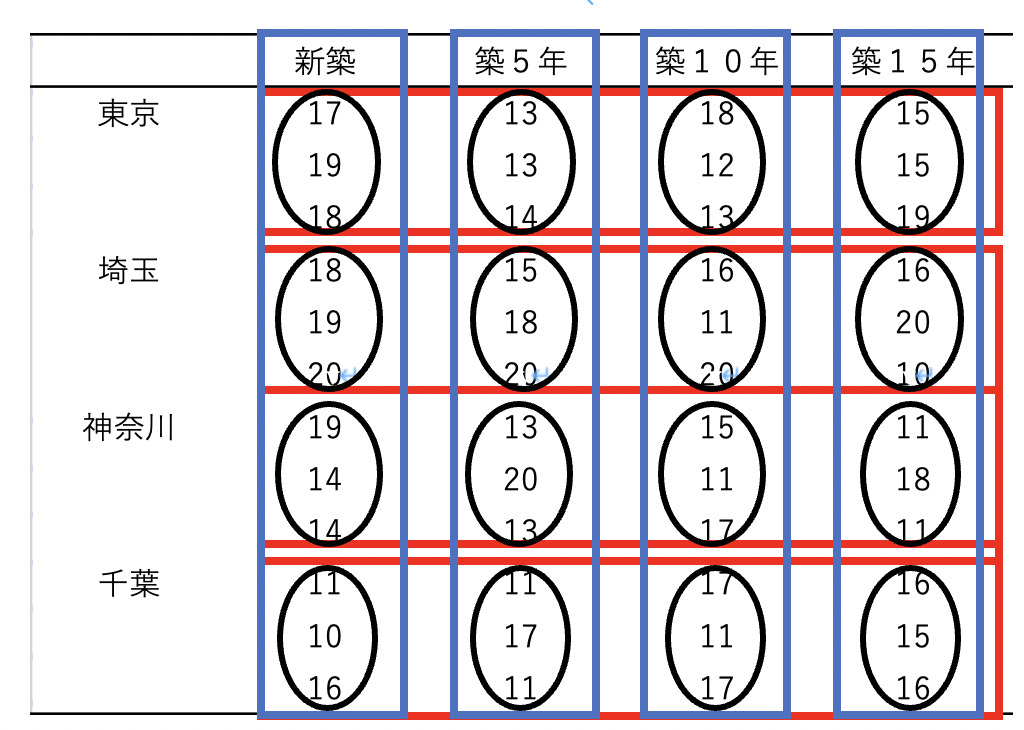
・全体の平均値：上のデータ全ての平均値
・図の赤い四角の部分：都道府県ごとの平均値です。
・図の青い四角の部分：築年数ごとの平均値です。
・図の黒い丸の部分：交互作用のための平均 (都道府県×築年数)です。
この４種類の平均値のそれぞれの差分を取っていくのが次のステップです！
step2 平均値同士の平方和を求める
次にそれぞれの平均値同士の差分から、平方和を求めます。
平方和とは二乗の和のことです。
↑の色塗り部分を埋めていきます。
・都道府県の平方和：「全体の平均値 ― 都道府県の各平均値」の平方和：
都道府県の違いが平均値に影響するか？をみています
・築年数の平方和：「全体の平均値 ― 築年数の各平均値」の平方和：
築年数の違いが平均値に影響するか？をみています
・都道府県×築年数の平方和 「全体の平均値 ― 交互作用の平均値」の平方和：
ここでは都道府県×築年数の交互作用を見ていますね。
・全体の平方和：「全体の平均値 ― 各データ」の平方和：
全体の平均と各データのズレを平方和にしたもの。
・残差の平方和
全体の平方和から各条件の平方和と交互作用の平方和を引いたものです。
残差は偶然生じた誤差として考えられており、後々の検定で重要になってきます。
step3 自由度を求める
全体、都道府県、築年数、都道府県×築年数の自由度をStep2と同様に求めていきます。
自由度とは自由に決められる値のことで、「サンプル数 – 1」の値になります。
詳しい説明は、「あパーブログ」がわかりやすかったです。
リンクを貼らせて頂きます。
こちら
・全体の自由度は「全データ – 1」←この場合は 48-1
・都道府県の自由度は「都道府県数 – 1」←この場合は 4-1
・築年数の自由度は「築年数 -１」←この場合は 4-1
・都道府県×築年数の自由度は「(都道府県数 -1) × （築年数 -1）」←この場合は 3×3
という具合に求められます。
・残差の自由度は全体の自由度からそれ以外の自由度を引いたものです。
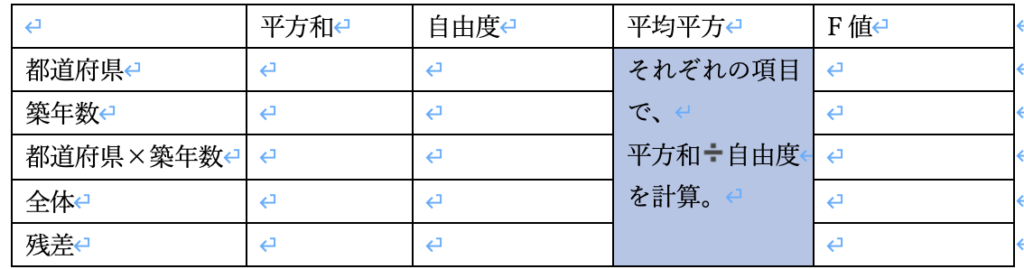
step4 平均平方を求める
次に、平均平方を求めていきます。
平均平方とは、step2で求めた平方和をstep3で求めた自由度で割った値です。
step5 F値を求める
そして最後にF 値を求めます。
このF値をもとに有意差のあり・なしを検定しているわけですね。
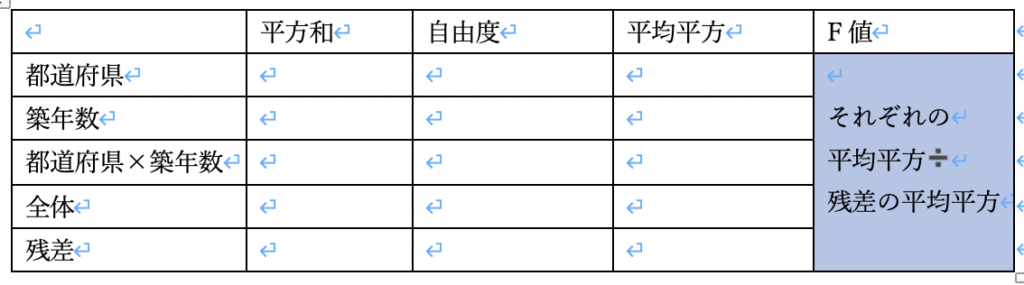
このF値を求めるために、残差の平均平方が重要な役割を持ちます。
つまり、F値は、これまで求めてきた平均平方を残差の平均平方で割って求めるんですね。
そのような疑問がありますよね。
その答えですが、、
残差の平均平方は偶然生じた誤差として考えられるからです。
つまり、偶然の誤差よりも十分に大きな差があることを統計的に検定したものが分散分析なんですね。
step6 F分布表を用いた検定
F分布表は自由度を参照して見ていきます。
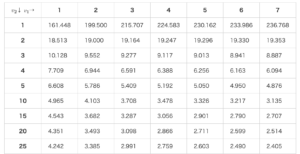
↑統計webより参照。 リンク
この図表だとv1, v2が自由度で、自由度5と10が交わる点にF値が来ていますね。
今回の例ですと、都道府県は４つの対象なので自由度3、そして残差の自由度3×3=9を確認し、F値を確認します。
求められたF値がF分布表で参照した数値よりも大きければ、有意差あり（偶然の誤差である可能性が否定される）ということです。
主効果と交互作用
この場合、都道府県で有意差がある、もしくは築年数で有意差があれば「主効果あり」と表現し、都道府県×築年数で有意差があれば「交互作用あり」と表現されます。
本日は以上です。
二限配置分散分析は、平均平方と自由度がポイントになっていることが伝わったでしょうか。
次回は二限配置分散分析の実装について記事にしていきます。
よろしくお願いします。
