こんにちは。
本日はこのような疑問にお答えしたいと思います。

本記事は特に研究の初心者である卒論生や院生に向け書きました。
この記事を読むことであなたの手持ちのデータにどのような解析方法が適しているのか、わかるようになります。

目的によって使う統計手法は違う
データはあるけど、この先どうしたらいいのかわからない。。
と途方に暮れている方はまず次の質問について考えてみて下さい。
あなたが示したいのは次のうちどれですか?
・データ間の差?
・データ間の関連?
・要因の調査?
どの目的を選ぶかによって選ぶ統計手法が変わってきます。
以下に説明を加えますね。
・データ間の差を調べる:検証したい仮説があり、それを確かめるときに用いる手法です。
例…朝型生徒と夜型生徒の試験成績を比較するなど。(仮説:朝型の方がいい)
・データ間の関連:2つのデータ間での相関性、関連性を見る手法です。
例:生活習慣と試験成績の関連性を検討します。
・要因の調査:ある項目の点数(or数値)に一体何が影響しているのかを調べます。手法としては回帰分析があります。
例:期末試験の成績に影響する要因には何がある(朝型/夜型、予備校通いの有無、授業態度etc)のだろう、と検討する。
大体の研究デザインは以上の3つに当てはまるのではないでしょうか。
(ただし応用的な手法は今回は省略しています)
ではそれぞれの説明を詳しく加えていきますね。
データ間の差を知りたい場合
2つのデータ間の数値比較を行っていくための方法を紹介します。
以下は例ですが、
あるAという薬の効果を調べるためにBという薬と比較する。
といった時に使用します。ABテストともいいます。統計手法を用いることで科学的で客観的な比較を行うことができます。
ABテストは以下のフローチャートで進んでいきます。
言葉の説明
データの尺度は?
名義尺度:あり:1、なし:2のような便宜的に数値をあてはめた尺度。
合計の群の数は?
2つのものを比較する場合と3つ以上を比較する場合で使用する統計方法が違います。
正規分布か?
正規分布:データの分布を見た時に左右対称の釣り鐘状の形になっているかという意味です。
対応のある
例えば食事前後の体重を比較するなど、同じ人やものの内での比較をする場合は対応があるになります。
対応のない
例えばA病院とB病院の治療成績を比較するなど他者との比較を行う場合は対応がないとなります。
詳しい実施方法は以前の記事でまとめました。
【SPSS】正規性を検定してt検定をする方法【10分でできる】
【R】Rでのχ二乗検定の方法です【データの尺度についておさえましょう】
2つの項目の比較をしたいときは上記の方法に沿って行いましょう。
データ間の関連を知りたい場合
次にデータ間の関連を調べる方法を書いていきます。
例えば、ラーメン店の売り上げと駐車場の広さの関係を見たいという場合はデータの関連を調べる必要がありますね。
そのようにデータの関連性を調べたい場合は、「相関係数」を使います。
相関係数は比較したいデータの尺度によって使用する方法が異なります。
・間隔尺度(比例尺度)と間隔尺度(比例尺度)の比較
→ピアソンの積率相関係数
間隔尺度とは等間隔性を持つもの(例:温度など)
比例尺度とは等間隔性を持ち、かつ原点も持つもの(例:長さ、高さなど)です。
・順序尺度を含むデータの関連ではスピアマンの順位相関係数を用います。
順序尺度とは便宜上の順位に分けた数です。(例:痛さを示す指数0-10など)
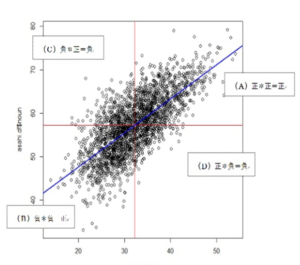
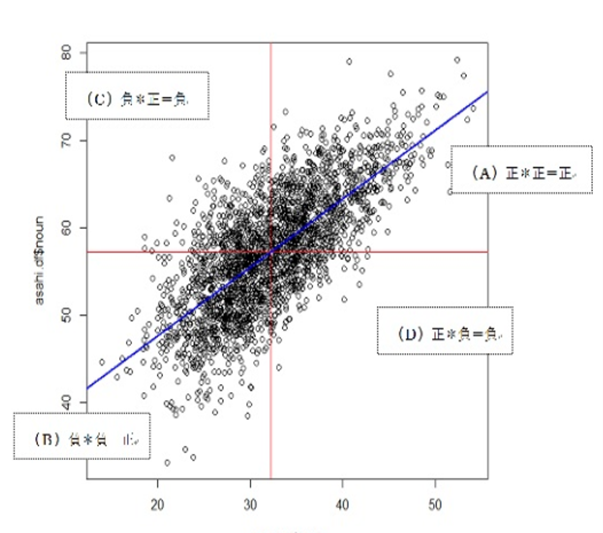
↑ピアソンやスピアマンの相関係数ではこのような「散布図」が描けます。
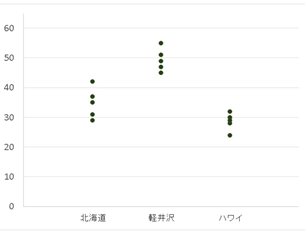
・名義尺度を含むデータの関連では相関比を用います。
名義尺度とは便宜上、数値を当てはめただけのものです。(例:男1、女2など)
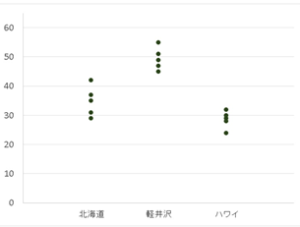
↑相関比ではこのような「散布図」が描けます。
相関解析の詳しい方法は以下の記事でまとめました。
【SPSS】SPSSを使う相関解析の方法 【約5分で読める】
2つの項目の関連を知りたい場合は、上記の方法に沿って行いましょう。
要因を知りたい場合
あるデータがあり、その要因を調べる場合です。
例えばラーメンの売り上げに影響するのは町の人口か、自動車の往来数か、その町の平均年齢か、近隣の店舗の数か…etcを調べる場合などですね。
目的変数と説明変数とは
回帰分析の考え方と基本用語を紹介します。
まず改善したいデータを決めます。
お店の売り上げなどですね。これを目的変数といいます。
次にこの目的変数への影響を調べたいデータを決めます。
これを説明変数といいます。
回帰分析は説明変数の数によって「単回帰分析」、「重回帰分析」に分類できます。
単回帰分析 【相関解析と似てる】
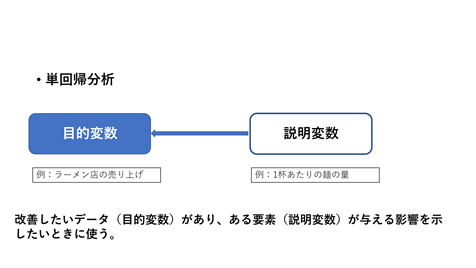
↑このように目的変数が1つ、説明変数が1つの場合は単回帰分析です。
データセットの例としてこんな感じです。
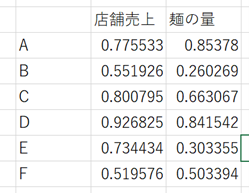
↑A~Fの店舗の麵の量(説明変数)が店舗売上(目的変数)に与える影響を明らかにできます。
詳しい回帰分析の方法については以下の記事をご覧ください。
【初心者向け】Rを使った単回帰分析【lm関数を修得】
単回帰分析では相関解析と同様、散布図を引けます。
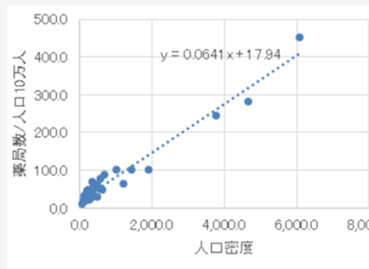
↑単回帰分析ではこの図のような散布図を引くことができます。
この散布図では薬局の数と人口密度との関係を見ているようです。
散布図の見方
右肩上がりの散布図:一方が上がればもう一方も上がる
右肩下がりの散布図:一方が上がればもう一方は下がる
このように、2つの変数間の関連を見ていくのが単回帰分析になります。
重回帰分析
重回帰分析は以下の使用方法になります。
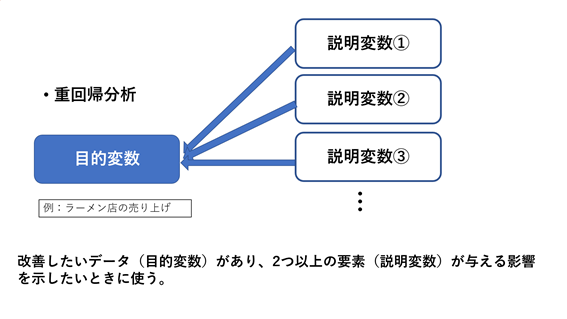
例えば、飲食店の数には人口が関わるのか、駅の数が関わるのかを調べたいというときに使います。
実際にRで重回帰分析を行うと以下のような結果が出てきます。見づらいですよね。、
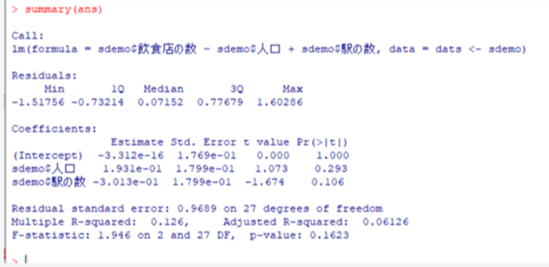
↑左下のEstimateというのが、それぞれの要素が目的変数にどの程度影響をしたのかを表しています。右端のp値が0.05を下回っていれば、有意に影響を及ぼしていた(影響を与えないとは言えないと証明される)と解釈できます。
このように、重回帰分析は2つ以上の要素が目的変数にどの程度影響するのかを検証することのできる手法です。
詳しい方法は以下の記事を参照ください。
Rを使った重回帰分析【初心者向け】