線形回帰とリッジ回帰の理論をまとめてみた

皆様も業務で機械学習を触れることが増えてきたかと思います。
AIを使用し、コーディングも容易にできるようになってきました。

ただ、このような時こそ処理の内容をわかりやすく説明する「説明力」が重要になっていることを感じます。機械学習についても、その背景を理解する重要性は増してきているのではないでしょうか。

今日は線形回帰とリッジ回帰の違いについてまとめました。

結論、リッジ回帰は外れ値への反応を抑えることができるメリットがあります。
アルゴリズムを理解しながらまとめました。

参考文献：
加藤公一, 2018, 機械学習のエッセンス

書籍URL

線形回帰について

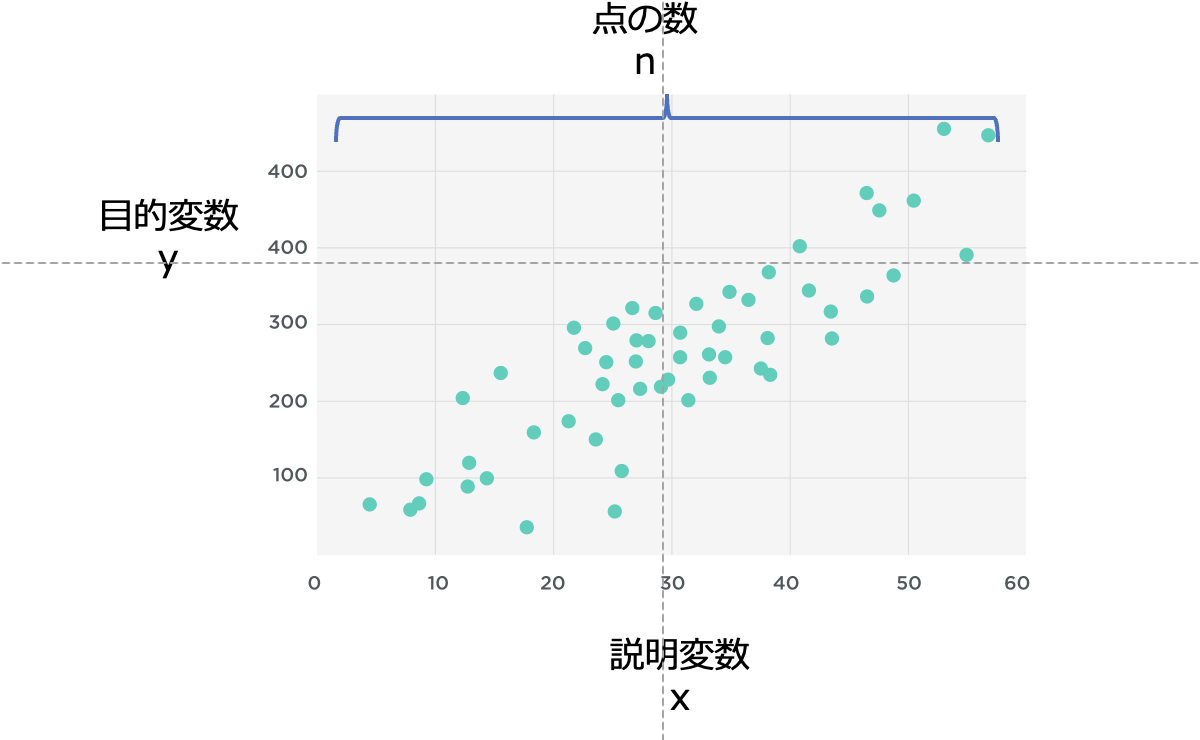
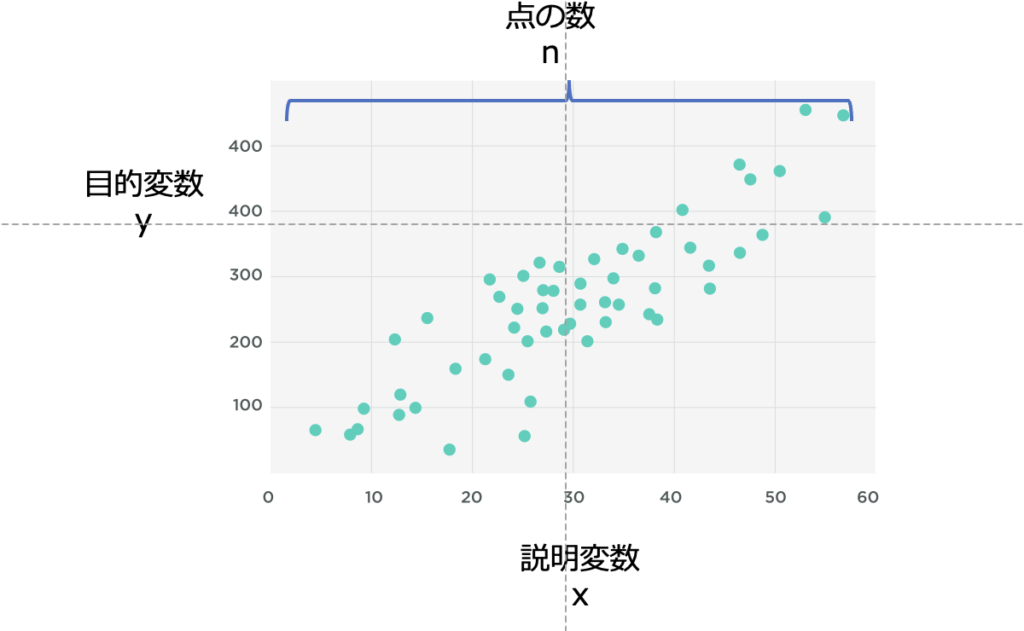
一次の回帰式によって、目的変数(y)を説明変数(x)で近似します。
例を挙げると、yが売上、xが気温で、気温xから売上yを予測する取り組みです。

$$y = a x + b + \varepsilon$$

ここでaは直線の傾き (回帰係数といいます)、bは切片です。aの絶対値が大きいほど(0から離れるほど)、説明変数xのyに対する影響が大きいと考えることができます。

回帰係数の求め方の説明

説明変数xのとりうる全ての点をnとすると、回帰式と目的変数yの誤差Eは下記のように表されます。

\[
E = \left( a x_i + b – y_i \right)^2
\]

回帰式は目的変数をなるべく正確に予測することが目的ですから、この残差Eは小さいほど良く、E = 0になるような回帰係数を求めていきます。

n個のデータのうち、i番目の特徴量xを表すため、xiとなっています。
ここで、E = 0とするようなa, bを「偏微分」を使って求めるというのが回帰式の係数を求める方法になります。

$$\frac{\partial E}{\partial a} = 0$$

$$\frac{\partial E}{\partial b} = 0$$

多項式の微分の際には、「合成関数」の知識を使います。
（合成関数とは？という方は、そんなに難しくないのでぜひ調べてみてください。）

(1)をaで偏微分すると、
$$
\sum_{i=1}^{n} x_i (a x_i + b – y_i) = 0
$$
(1)をbで偏微分すると、
$$
\sum_{i=1}^{n} (a x_i + b – y_i) = 0
$$

この２式を連立方程式で解くことで、回帰係数と切片a, bを求め、 y = ax + bの式に代入しyを求める。というのが線形回帰式での回帰係数を求めるアルゴリズムです。

説明変数が多次元の場合の回帰係数の求め方の説明

上記は説明変数（例：気温）が１つの場合ですが、２つ以上ある多次元の場合（例：気温、日付、天気など）も基本は同様です。

回帰式は

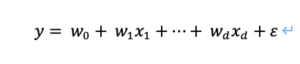
で表せ、yが目的変数、xが説明変数のベクトル、wがそれぞれの回帰係数のベクトルです(εは誤差)。ここでxベクトル(x1,x2… )の最初に「1」を追加し、同時にベクトルwの最後に誤差項εを追加することで行列式が下記のようにすっきりします。

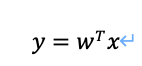
ベクトル同士で「T」を挟むと、ベクトルとベクトルの掛け算をするという意味です。
先ほどと同様に

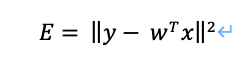
としたときの、残差Eを0にするようなwを求めていきます。
上式を展開し、wで偏微分をしていきます。
なお、ここで▽は「勾配」を指しており、「偏微分の結果を並べたベクトル」のことです。
Eをwで偏微分した勾配が0になるようなwを求めます。

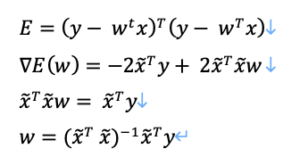
となり、回帰係数wを求めることができます。

リッジ回帰

線形回帰の時に使用した残差を最小化する式にハイパーパラメータλ(ラムダ)を追加したものです。λを回帰係数wにかける項を追加したことにより、回帰係数wが大きくなることを防ぐ作用を持っています。

$$
E(w) = \| y  –  \tilde{x} w \|^2 + \lambda \| w \|^2
$$

展開すると、

$$
E(w) = (y – \widetilde{x} w)^\top (y – \widetilde{x} w) + \lambda w^\top w
$$

これをwで偏微分すると、

$$
\nabla E(w) = -2 \widetilde{x}^\top (y – \widetilde{x} w) + 2 \lambda w = 0
$$

それを変形していき、下記のようになります。

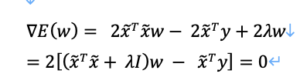
ここで、Iは単位行列(対角成分が1, それ以外は0)です。
よって、ここからwを求めると

$$
w = (\widetilde{x}^\top \widetilde{x} + \lambda I)^{-1} \widetilde{x}^\top y
$$

となります。
通常の線形回帰の際のwの等式と比較し、λIが含まれているのが違いですね。

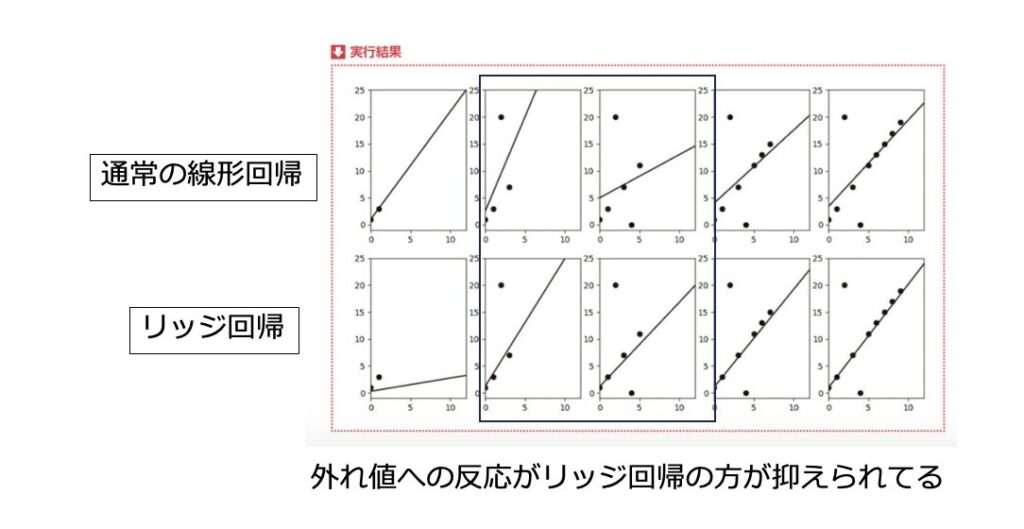
下図は、データを１つずつ追加したときの線形回帰とリッジ回帰の挙動の違いです。
線形回帰が上行、リッジ回帰が下行です。
２、3列目でそれぞれ平均より上、下への外れ値的なデータが追加されたとき、線形回帰は傾きが大きく上下するのに対して、リッジ回帰では変動を抑えられています。

Screenshot

機械学習のエッセンス P207より一部改変

つまり、リッジ回帰を用いることで、外れ値的なデータの影響を抑える(数式上の回帰係数wの変動が抑えられている)ことがわかります。

まとめ