こんにちは。
本日はRを使って散布図を書く方法を記事にしました。
散布図は2つの項目間の関係性を確認するときに非常によく使う図ですね。
✅疑問
・Rでデータを視覚化する方法がわからない
・Rで散布図や回帰直線の引き方を知りたい
このような疑問に答えます。
僕は医療職で働きながら大学院に通って4年目です。SPSSやRを使って学会発表や論文投稿まで行うことができています。
✅このような方におススメ
・Rを使ってデータを視覚化したい
・Rを始めたばかり。基礎的な使用法を身に着けたい
では始めていきます。
ちなみに、Rを使った棒グラフの作り方については以前記事にしています。参考にしてみてください。
Rでデータの概要を表示する、棒グラフを作成する 【基礎編】
Rを使った散布図の書き方【簡単です】
本日はこちらのdemodataを使用します。
こちら

↑
9つの項目がある30行9列のデータになっています。
このデータをRに読み込んでいきましょう。

↑read.csv関数を使います。
RでのCSVファイルの読み込み方法についてはこちらの記事を参照してください。
Rにexcelで作ったファイルを読み込む方法【CSV形式で読み込みましょう】
これでRにdemodataのCSVファイルが読み込まれました。
では早速散布図を作ってみましょう。
「背中角度」と「足の長さ」で散布図を作ってみます。

↑
関数の解説
・plot(A,B):AをX軸、BをY軸とした散布図を作る。

↑
散布図が完成しました。ただし、まだタイトルとかラベルはない状態です。
散布図を見やすくするオプション
ここで散布図を見やすくするオプションを紹介します。
参考:データ科学便覧
| オプション | 詳細 | 例 |
| type | プロットの形式を指定する
p : 点 i : ライン b : 点とライン n : プロットしない |
type=”p” |
| col | プロットの色を指定
blue, green, red, orange など |
col=”blue” |
| main | 散布図のタイトルを指定 | main=”demo plot” |
| xlab | x軸のラベルを指定 | xlab=”Aの角度” |
| ylab | y軸のラベルを指定 | ylab=”Bの点数” |
| xlim | x軸の表示範囲の指定。
ベクトル(c)で指定。 |
xlim=c(0,10) |
| ylim | y軸の表示範囲の指定。
ベクトル(c)で指定。 |
ylim=c(0,10) |
| log | xまたはyを指定すると指定した軸を対数軸で表示 | log=”y” |
| cex.main | グラフタイトルのフォントサイズの指定 | cex.main=”3” |
| cex.lab | 軸ラベルのフォントサイズの指定 | cex.lab=”1.5” |
| cex.names | 軸項目のフォントサイズの指定 | cex.names=”1.5” |
| cex.axis | 目盛りのフォントサイズの指定 | cex.axis=”1.2” |
散布図にタイトルやラベルを付ける
![]()
↑
<関数の解説>
col=”blue”: プロットを青色に変更
main=”demodata”: グラフタイトルをつけた
cex.main=”3”: タイトルのフォントを3にした
xlab=”背中の角度”: x軸のラベルにタイトルを付けた
ylab=”足の長さ”: y軸のラベルにタイトルを付けた

↑このような散布図ができました。
だいぶん見やすくなってきましたよね。
あとはこちらに回帰直線を引いていきたいと思います。
散布図に回帰直線を引く
回帰直線とは
単回帰分析の結果を示す線分です。
単回帰分析とは
y=ax+b
の一次方程式の形を求める分析です。
aが傾き、bが切片といいます
まずは単回帰分析を行う必要があります。

↑
関数の解説
lm(A~B):AとBの間の関係を求める。
Aはy軸(縦)のデータ、Bはx軸(横)のデータになるように注意です。
※逆に入れてしまうと回帰直線は出てきません。
次に回帰直線を引きます

↑
関数の解説
abline(A):Aの結果に沿った直線を引く関数
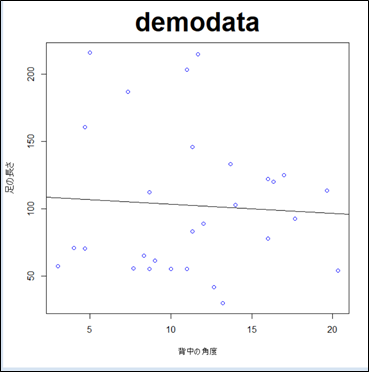
↑このような回帰直線が引けました。
【応用】回帰分析の結果を解釈してみよう
散布図を見ると回帰直線が右下に下がっていますよね。
つまり「背中の角度」が大きくなるほど足の長さが短くなるという傾向が読み取れます。
先ほどの回帰分析の結果を詳しく見ることができます。

↑
関数の解説
summary(A):Aの分析結果の詳細を表示する

↑
このような結果が出てきます。
真ん中あたりの「Coefficients」を見ます。
今回はx軸がdata[,5]ですので、その行を見ます。
「Estimate」が-0.6909になっていますね。これがy=ax+bのaの部分(傾き)です。
また、右側の「Pr」はp値を指します。p値は帰無仮説(傾きは0である)が生じる確率で、5%未満で有意な関係性です。
今回は0.752なので75%は傾きが0になる確率があるため有意な関係性ではありません。
このように結果を解釈します。
本日のまとめ
散布図はデータの関係性を視覚的に捉えるためよく使われる図です。
また、回帰直線を引きその結果を解釈できれば単回帰分析の知識までもカバーできています。
本日は以上となります。
今後も有益な記事を書いていきます。
よろしくお願いします。

