Rによる2群間検定　【4種類解説しました】

本日はこういった疑問に答えます。

これを書いている僕は
・大学院5年目
・ぶっちゃけRは中級者ですが、基本的な検定はできます。
・Rは０から初心者への移行が最も大変なので、分かりやすく書いていきたいと思います。

■1 2群間の比較を実際に行いましょう

この検定は最もよく使うのではないでしょうか？
但し、群間の比較には以下の4つがあります。
下記に一目でわかる表を貼りました。

ではこれからそれぞれ説明していきます。今回もデモデータをつかいます。

ダウンロードはこちらです。

①　対応のあるt検定（パラメトリック検定）

データの正規性が立証され、対応のあるデータであれば「対応のあるt検定」を行います。
コードは

例えば、デモデータの8行目、9行目のように全対象者にA条件、B条件を行ったときに対応のあるt検定を使います。各条件を1回ずつ、全員合計2回実施していますよね。

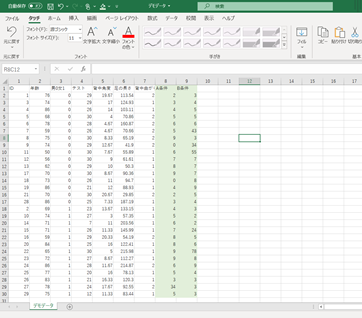
早速Rで行ってみましょう。

Rでt.test (x=data[,8], y=data[,9], paired=T)
と打ち込みます。
ここで[,8]と[,9]は横行を指定していません。
Rでは全ての行を選択するときは行数を省略可能です。
もしもこれを省略しない場合は、CSVファイルでは2行目～30行目なので、
t.test(x=data[1:29,8],y=data[1:29,9],paired=T)
となります。もし、この例のように全行指定したい場合はこの省略の仕方も覚えると便利です。

結果はp=0.1031が読み取れます。
P>0.05なので条件Aと条件Bに差がないという帰無仮説が成立します。

②　対応のないt検定

対応のないt検定は

ウェルチのt検定

とも言います。
データに正規性が確認され、対応のない（繰り返しのない）項目同士を比較する場合はウェルチのt検定を使います。
厳密にはステューデントのt検定というものもあるのですが、こちらは等分散を仮定するものとされ、最近は使わない流れのようです。
先ほどのコードとほぼ同じで、

var.equalとは等分散の有無を意味します。ウェルチの検定は等分散を仮定しないのでFalseのFを入れましょう。
paired=FはこちらもFalseなので「対応がない」ことを示しますね。

デモデータの5行目、背中角度を男女群間で比較してみます。

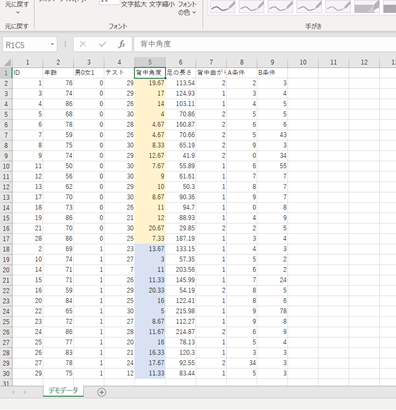
黄色が男性、青色が女性です。
3行目のデータは男女別に並んでいますでしょうか。もし、男女バラバラに並んでいたら、こちらの記事に並び替え方が乗っていますので、見てみてください。
Rでの正規性の検定　～Rの群間検定①～

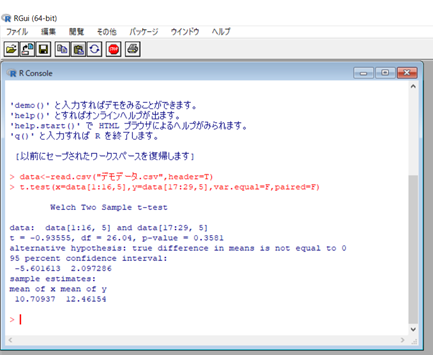
>t.test(x=data[1:16,5],y=data[17:29,5],var.equal=F,paired=F)

CSVファイルの背中の角度は、男性が横2行目から17行目で女性が横18行目から30行目です。

先頭行はカウントされていないので1行分マイナスしてRに入れて下さい。
なので男性はdata[1:16,5]で、女性はdata[17:29,5]です。「：」は「～」を意味します。

これでEnterを押すと結果が出ます。
p値は0.359なので
「男性と女性の背中の角度には有意差がない」ことがわかりましたね。

③　ウィルコクソンの順位和検定　（対応のない場合）

さて、ウィルコクソンの順位和検定を行う場合ですが、

Rではまずウィルコクソンを実施できるパッケージをダウンロードする必要があります。このあたりはSPSSと比べて面倒な作業ですが、下記のコードをコピペして貼り付けてくれればすぐ終わります。
（参考：データ科学便覧）

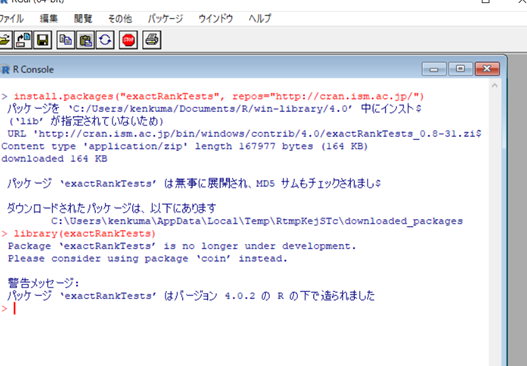
こんな感じで「あれ、うまくいってない？！」という表記が出ますが、問題ありません。

今度はデモデータの「足の長さ」について男女差を調べてみましょう。

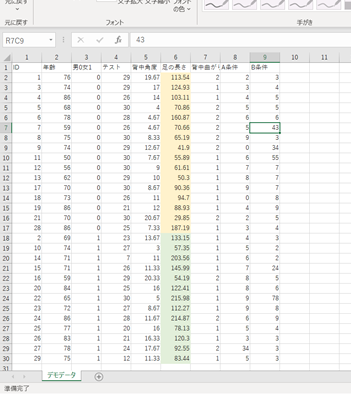
ウィルコクソンの順位和検定を行うコードは

です。対応のない検定なのでpaired=Fになっていますね。

実際にはこんな感じ。

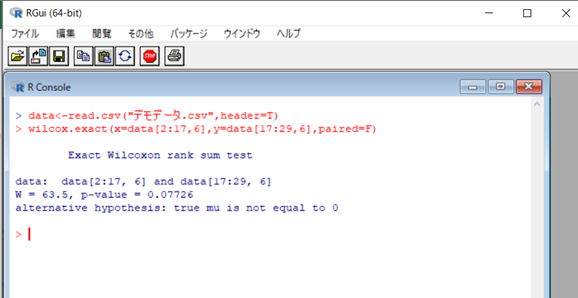
行の範囲は「：」で表すことは大丈夫ですかね。「～」と同じ意味です。P=0.07なので、有意差はないです。「足の長さに差がない」という帰無仮説が採択されました。

④　ウィルコクソンの符号順位検定　（対応のある場合）

こちらはウィルコクソンの順位和検定の対応あり版で、

と、PairedのところのFalseのFをTrueのTに変えるだけです。
デモデータで試してみましょう。
8列目のA条件と9列目のB で比較します。

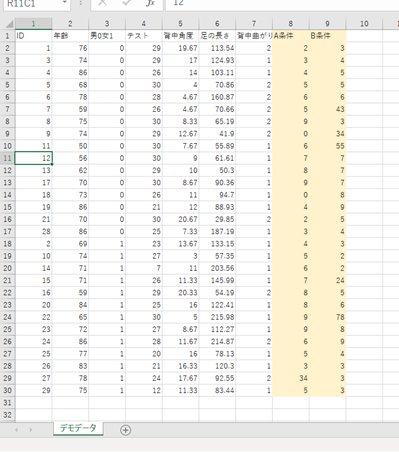
コードは

wilcox.exact (x=data[,8],y=data[,9],paired=T)

となります。

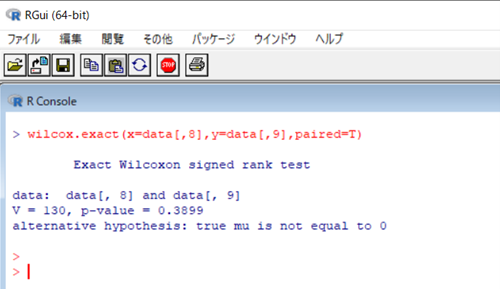
ここで[,8]と[,9]は横行を指定していません。（先ほどと同じ説明を一応乗せておきます）

Rでは全ての行を選択するときは行数を省略可能です。
もしもこれを省略しない場合は、CSVファイルでは2行目～30行目なので、
wilcox.exact (x=data[1:29,8],y=data[1:29,9],paired=T)
となります。もし、この例のように全行指定したい場合はこの省略の仕方も覚えると便利です。
結果はp-valueを見てもらえると、0.3899なので帰無仮説「条件Aと条件Bに差がない」を支持します。

今日は以上です。
これからも有益な記事を書いていきたいと思います。
よろしくお願いします。