こんにちは。本日はSPSSを使って3群以上のデータを比較する方法を説明します。
2群の比較であれば以前紹介したt検定やウィルコクソンの順位和検定でできますが、3群以上では方法が変わります。
2群の比較
【SPSS】t検定のやり方
【SPSS】マンホイットニーのU検定、ウィルコクソンのの符号付き順位和検定
✅疑問
・SPSSで3群以上の検定ってどうすればいいの?
・いろんな方法をまとめてほしい
このような疑問に答えていきます。
僕は医療職で働きながら大学院に通って4年目です。統計学初心者からSPSS、Rを使って学会発表や論文投稿までできるようになりました。
では始めていきます。
3群以上の比較に使う方法【4種類】【SPSS】
3群の比較とは例えば以下のような状態です。
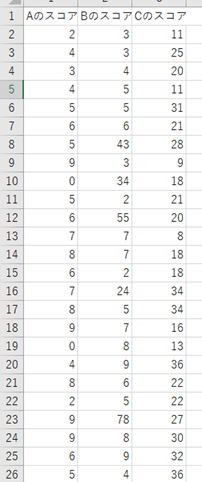
A,B,Cの3グループでグループ間に差があるのか否かについて検定します。
3群の比較では以下の4つの手法があります。
| パラメトリック | 対応あり | 反復測定一元配置分散分析 |
| 対応なし | 一元配置分散分析 | |
| ノンパラメトリック | 対応あり | フリードマン検定 |
| 対応なし | クラスカルウォリス検定 |
<用語解説>
パラメトリック:正規分布している意味で、データの比較は平均値を用います。
ノンパラメトリック:正規分布していないことで、データの比較には中央値を用います。
対応あり:同じ対象者による繰り返しデータの意味です。
例:1名の対象者でA,B,Cの3条件を繰り返したときの条件間比較をする
対応なし:同じ対象者による繰り返しではないデータです。
例:東京とニューヨーク、ロンドンの3都市で年間の平均気温を比較する
注意点
その1 解釈の注意点
✓ これらは「3群間に差があるかどうか」を検定するもの
✓ わかることは「3群に差があるか」だけ
✓ どれとどれに差があるかについては多重比較(その後の検定)が必要です。
初心者の方はここでは「詳細な解析は多重比較というものでやるんだな~」と思っていてもらえれば大丈夫です。
その2【前処理】Excelデータの行列を入れ替える
SPSSでの一元配置分散分析ではデータを縦(列)方向に並び変えなくてはなりません。
こういう処理をすることを「データの前処理」といったりします。
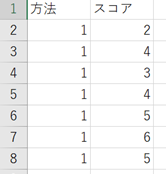
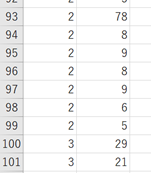
↑
このような縦1列に3群が並んでいる状態を作ることが必要です。
一方で反復測定一元配置分散分析ではデータを横方向に並び替える必要があります。
少しめんどくさいのですが、注意しましょう。
その3【文字は数字に変換する】
一元配置分散分析(対応なし)のときは、上に書いてあるような「Aのスコア」というような文字分類だとSPSSが上手く読みこまないです。なので以下のように変更します。
「Aのスコア」→「1」
「Bのスコア」→「2」
「Cのスコア」→「3」
一元配置分散分析【パラメトリック・対応なし】
まずデータの読み込みを行います。

↑
一元配置分散分析ではデータは縦方向です。
SPSSへのデータの読み込みはこちらの記事を参考にして下さい。
SPSSでExcelファイルやCSVファイルを読み込む方法 【まずこれを覚えましょう】
一元配置分散分析の実行

↑「分析」→「平均の比較」→「一元配置分散分析」です。

↑このような画面になります。
見たい変数(このデータの場合「スコア」)を「従属変数」に移します。
群分けをしている「因子」を「因子」に移します。
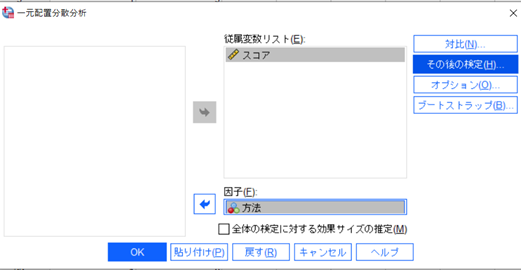
↑
「その後の検定」をクリックです。
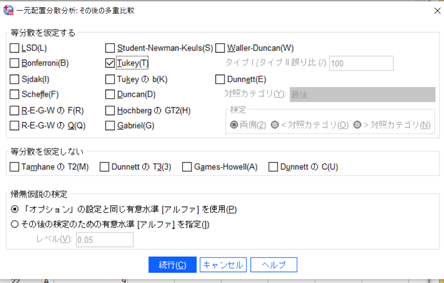
↑
「Turkey」をクリックします
「Turkeyの多重比較」は3群間に有意差があった場合に、具体的にどこに有意差があるのかを出してくれます。

↑
次に「オプション」をクリックです。

↑
「記述統計量」、「等分散性の検定」、「Welch検定」にチェックを入れます。
<用語解説>
「記述統計」:各群の平均値や標準偏差、個数を出してくれます。
「等分散性の検定」:各群の分散が等しいのかどうかを検定します。
分散=(各データ数値-平均値)2です。
「welch検定」:等分散が否定された場合、welch検定の結果も見ます。
一元配置分散分析の結果を確認する
step1等分散性の確認
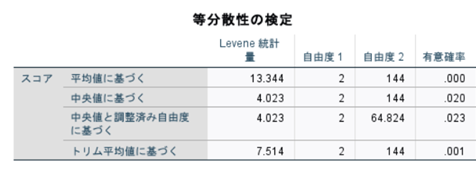
↑まず等分散性を確認します、「平均値に基づく」の部分を見てもらうと、有意確率[0.000]で帰無仮説である「説明変数は等分散しない」が棄却されました。有意に等分散するといえます。
✓等分散していたら step2 一元配置分散分析へ
✓ 等分散してなかったら step3 welch検定へ
step2分散分析結果の確認
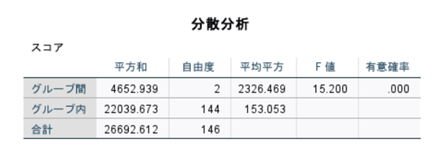
↑分散分析の結果です。一番左列の「グループ間」で「有意確率」を見ます。
帰無仮説は「各条件間に差はない」です。有意確率が0.05を下回っていますので有意に条件間に差があるということが言えます。
step3 welch検定結果の確認
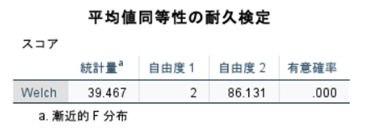
↑welch分析の結果です。等分散が否定された場合に確認します、「有意確率」の欄を見ます。
【分散分析で有意差があれば】多重比較の結果を確認
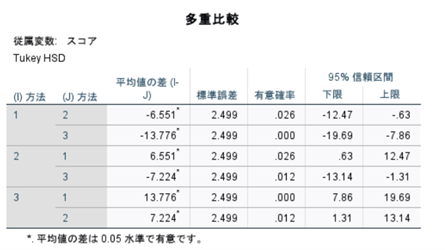
↑Turkeyの多重比較結果です。
Turkeyの比較によってペアごとの比較が確認できます。
「1」は「2」、「3」ともにp<0.05の有意差がありますね。
「2」も「1」、「3」ともにp<0.05の有意差がありますね。
これで一元配置分散分析は終わりです。
反復測定一元配置分散分析【パラメトリック・対応あり】
反復測定一元配置分散分析の注意点【データの並べ方】
反復測定一元配置分散分析を行う場合、データの並べ方が「一元配置分散分析」のときと違います。
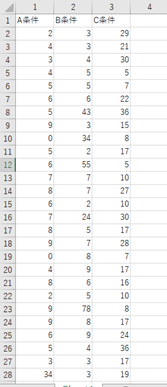
↑
このように「横並び」にしてください。
データの並べ方のポイント
✓ 「一元配置分散分析」は縦並び
✓ 「反復測定一元配置分散分析」は横並び
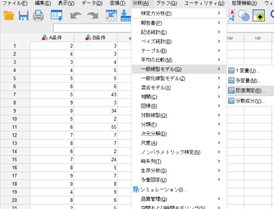
↑
「分析」→「一般線形モデル」→「反復測定」を選択します。
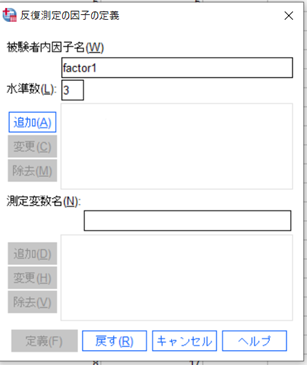
↑
このような画面が出ますので「被検者内因子名」、「水準数」を記入します。
今回は3条件なので「3」を入力します。
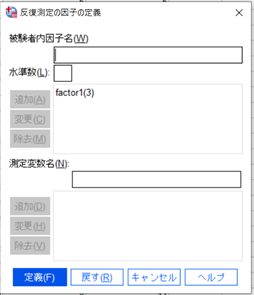
↑
「追加」ボタンを押すと上の画面のような表示になります。
「定義」を押してください。

↑
このような画面になります。3つの列(条件)を「被検者内変数」に張り付けましょう。
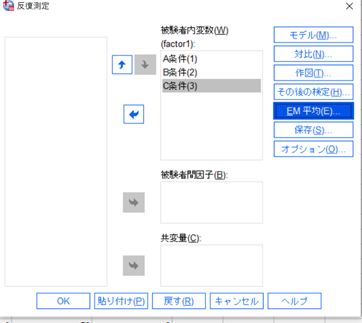
↑次に「EM平均」をクリックです。

↑「因子と交互作用」に「factor1」(要素名)が出てくるので、「平均値の表示」に移します。
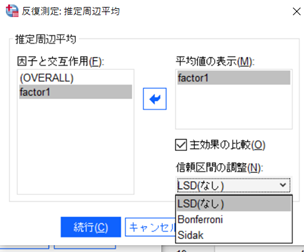
↑
次に「主効果の比較」チェックボックスにチェックします。そして「信頼区間の調整」を押します。ここは多重比較を選べます。「Bonferroni」、「Sidak」から選べます。
解説
✓ 多重比較
3群以上の比較では結局どの群とどの群に比較があるかはっきりさせるため、t検定を繰り返します。しかしt検定を繰り返す場合はp値を調整しなくてはいけません。
本当は有意差がないのに有意差ありと判定してしまう「第Ⅰ種の過誤」を防ぐために必要です。
✓ Bonferroniの多重比較
最も厳格な多重比較です。それぞれ群間の検定で出たp値を単純に個体数で割ります。
p値/個体数です。
ここまで来たら「OK」を押します。
反復測定一元配置分散分析の結果を確認

↑
Mauchlyの球面性の検定をまず確認します
この有意確率が0.05未満かどうか確認し、次に行きます。
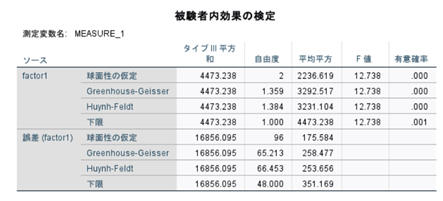
↑「被検者内効果の検定」を見ます。
Mauchlyの球面性検定が0.05未満→「球面性の仮定」を見て下さい。
Mauchlyの球面性検定が0.05未満→「Greenhouse-Geisser」を見て下さい。
有意確率が0.05未満であれば「3群のどこかに有意差あり」となります。
次に多重比較の結果を確認します。
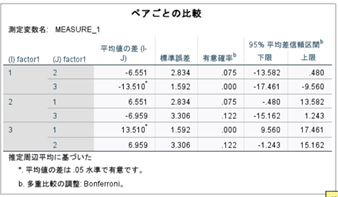
↑「ペアごとの比較」を確認します。
ここでそれぞれの条件間を比較できます。
多重比較は今回は「Bonferroni」を設定しました。
本日は以上となります。
これからも有益な記事を書いていきます。
よろしくお願いします。

