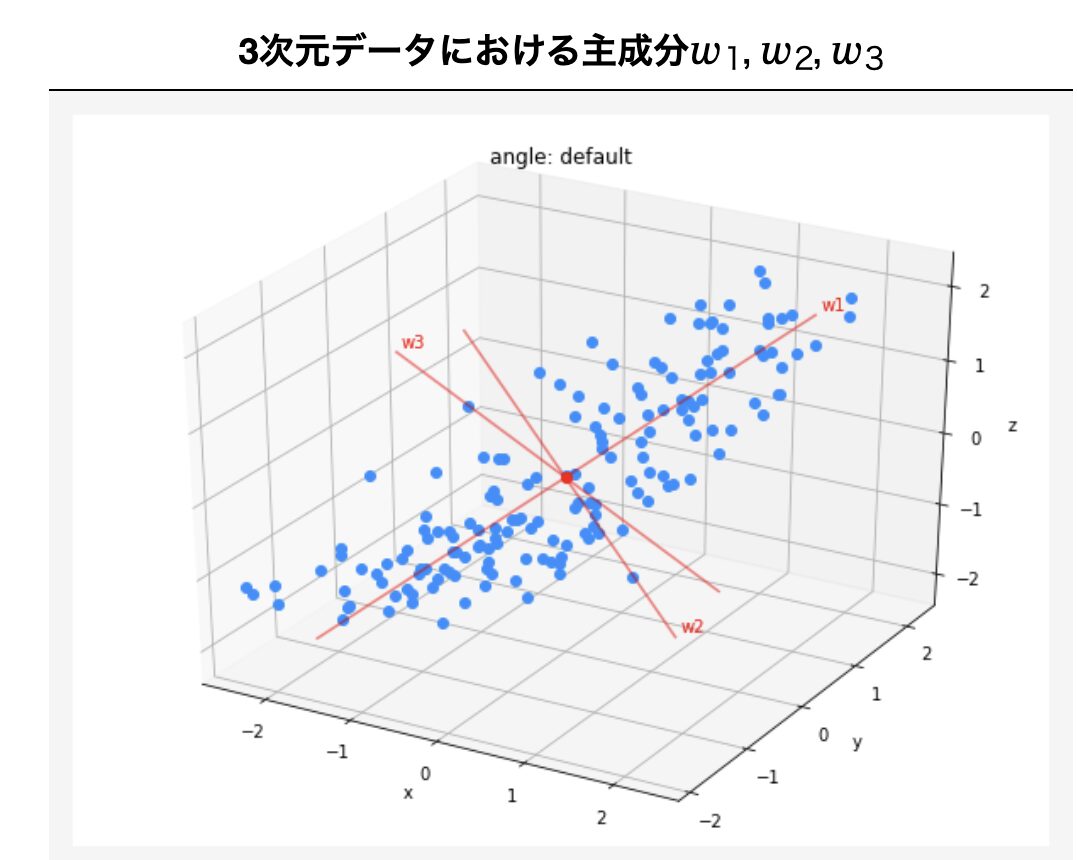
今回は主成分分析についてまとめてみました。
主成分分析を実務で使うメリットは何でしょうか?
以下のメリットがあると考えられます。
- 複雑化したデータを解釈可能にする(次元削減)
- 通常の検定ではわからない新しい視点を発見でき
- それぞれのデータ分析の軸(切り方)にはどの特徴量(項目)が効くのか、主成分スコアから考察できる
つまり、眺めていては何もわからないような複雑データを説明可能なレベルへ落とし込むことができます
次元削減とは
複雑な多次元のデータを低次元に削減することです。
例えば、30個の項目からなるデータがあるとします。
通常の検定では、30個の次元(30個の検定)を行いますが、「結局どの項目が重要なのか」、客観的に表す方法がありません。
主成分分析を行うことで、複数の特徴量を加味した2~3の軸にまとめることができます。
次元の削減は、あるルールに従います。
ことです。
イメージ画像:下記のように多次元のデータをより少ない次元に削減します
Screenshot
なぜ分散を最大化するのか?
データの分散が最大化するということは、各々のデータがみんな違う、つまり異なる特徴を持つことを意味します。
なぜ、データ同士が異なる特徴を持つ方がいいのでしょうか?
• 各々のデータが持つ特徴の強さ(情報量)が大きい
ことを意味します
逆にもし、分散を小さくしてしまうと、各々のデータが近しくなり、情報量も小さくなってしまいます。
加えて、削減後データから実データを復元する際にも、各データの分散が大きい方がより高い精度で復元できると言われています。
数式で理解
実データ行列をX、次元削減後のベクトルをw1とします。このw1を主成分といい、2つ以上の主成分が作成されます。ここではw1を第1主成分と仮定し進めます。
実データ行列Xとある主成分w1をかけた平均と分散を求めていきます
実データ行列Xの平均値にw1をかけた値です
\[
\frac{1}{n} \sum_{i=1}^{n} w_1^{\top} x_i
= \frac{1}{n} w_1^{\top} \sum_{i=1}^{n} x_i
= w_1^{\top} \bar{x}
\]
\[
\frac{1}{n} \sum_{i=1}^{n} \left\| w_1^{\top} x_i – w_1^{\top} \bar{x} \right\|^2
\]
2乗の部分を展開して、
\[
\frac{1}{n} \sum_{i=1}^{n}
\left\{ w_1^{\top} (x_i – \bar{x}) \right\}
\left\{ w_1^{\top} (x_i – \bar{x}) \right\}
\]
w1の部分を外に出すと
\[
w_1^{\top}
\left\{
\frac{1}{n} \sum_{i=1}^{n}
\left( x_i – \bar{x} \right)
\left( x_i – \bar{x} \right)^{\top}
\right\}
w_1
\]
ここでw1に挟まれる下記部分はxiの共分散行列になります。
この実データの共分散行列をSと定義します
共分散行列とは、あるベクトルのばらつきを表す行列です。
\[
S
= \frac{1}{n} \sum_{i=1}^{n}
\left( x_i – \bar{x} \right)
\left( x_i – \bar{x} \right)^{\top}
\]
最適化問題(固有値問題)へ
主成分分析はデータの分散を最大化するようなベクトルを求めていく取り組みであるので、下記のような最適化問題へ変換できます
\[
\begin{aligned}
\text{maximize} \quad & w_1^{\top} S w_1 \\
\text{subject to} \quad & w_1^{\top} w_1 = 1
\end{aligned}
\]
ここでなぜ、w1同士の積が1になるのでしょうか。これは1として定めているためです。
ベクトル同士のかけ算(内積)はそのベクトルの大きさ(長さ)を示します。
この長さは無限にとりえますが、そうすると求めたい分散も無限大になってしまうので
長さは1と定めています(参考文献とは)。
つまりラグンジュ乗数という新しい変数λ1を追加します。
\[
\phi(w_1, \lambda_1)
= w_1^{\top} S w_1
– \lambda_1 \left( w_1^{\top} w_1 – 1 \right)
\]
φをw1について偏微分します
\[
\frac{\partial \phi}{\partial w_1}
= 2 \left( S w_1 – \lambda_1 w_1 \right) = 0
\]
\[
\therefore \quad
S w_1 = \lambda_1 w_1
\]
という固有値問題になります。
Sはデータから作られる共分散行列なので既知の行列で、w1が第1主成分であるときに上記の式をみたしつつ、Sが最大になるλ1を求めることがここでの固有値問題です
λを大きい順に並べる
今までの流れで複数の軸の主成分ベクトル(wi)が作成されます。それぞれの主成分ベクトルには対応する固有値λiが存在しています。理解のポイントしては
実務scikit-learnでのアルゴリズム
今まで書いたのが、基本のアルゴリズムですが、実務上では実データ行列Xに対し特異値分解をしてPCAを行います。
特異値分解とは
実データ行列をXとすると
\[
X = U \Sigma V^{\top}
\]
というように分類することです。ここでUを左特異ベクトル、Σを特異値、Vを右特異ベクトルと言います。特異値が先ほど説明した固有値に対応し、Vが主成分ベクトルになります。
特異値分解の意味
Vは行列であり、その各列が右特異ベクトルというベクトルで構成されています。この右特異ベクトルが主成分ベクトルに当たります。ほとんどの場合、2つ以上のベクトルが存在するでしょうが、それぞれのベクトルは独立(直交、内積が0、相関しない)しています。
Σは特異値であり、一言で言うと固有値を行列化したものです。主成分ベクトルである右特異ベクトルの各成分の寄与度を表していると説明できます。
データの行数が万を超えるようなことも多い実務上では、固有値分解を行うと計算コストが高く、結果が不安定になるようです。そこで実データ行列から固有値分解を行なって主成分を抽出します。この詳細なアルゴリズムは成書をご参照ください。
Pythonコード
上記で説明したPCAの結果の解釈
explained_variance_ratio_:各成分の寄与度 componetnts:その成分の中で、各特徴量の寄与度を示すimport numpy as np
from sklearn.decomposition import PCA
# サンプルデータをXとする
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
X
pca = PCA(n_components=2)
pca.fit(X)
# explained_variance_ratio_:各主成分が全ての分散のどの程度
# を占めるか(割合)
print(pca.explained_variance_ratio_)
# [0.99244289 0.00755711]
# 累積寄与率に変換
np.cumsum(pca.explained_variance_ratio_)
# array([0.99244289, 1. ])
# 主成分の軸成分(主成分ベクトル)
# 各特徴量が成分に貢献する程度を示す
# 成分数 * 特徴量数(列数)
pca.components_
# array([[ 0.83849224, 0.54491354],
# [-0.54491354, 0.83849224]])
print(pca.singular_values_)
# 元サンプルに主成分ベクトル(components_)をかけたもの
pca.transform(X)
# array([[-1.38340578, -0.2935787 ],
# [-2.22189802, 0.25133484],
# [-3.6053038 , -0.04224385],
# [ 1.38340578, 0.2935787 ],
# [ 2.22189802, -0.25133484],
# [ 3.6053038 , 0.04224385]])