こんにちは、本日はSPSSでのノンパラメトリックな3群以上の比較について記事にしました。
前回は、パラメトリックな3群以上の比較を紹介しました。
前回記事
【SPSS】3群以上の比較 【一元配置分散分析、反復測定一元配置分散分析】
3群以上の比較は4種類あるのでした。
| パラメトリック | 対応あり | 反復測定一元配置分散分析 |
| 対応なし | 一元配置分散分析 | |
| ノンパラメトリック | 対応あり | フリードマン検定 |
| 対応なし | クラスカルウォリス検定 |
✅疑問
・SPSSを使ったノンパラメトリック検定で3群以上の検定ってどうすればいいの?
・ノンパラメトリックでの3群比較はどういう方法があるの?
このような疑問に答えていきます。
これを紹介する僕は医療職で働きながら大学院に通って4年目です。
統計学初心者からSPSS、Rを使って学会発表や論文投稿までできるようになりました。
わかりやすく説明していきますね。
ノンパラメトリックで3群以上の比較に使う方法【SPSS】
【パラメトリック・ノンパラメトリックとは?】
それぞれの変数(データ)の分布が正規分布(釣りがね型の分布)しているかどうかの分類です。
正規性といいます。
SPSSでの正規性の確認方法は以前記事に乗せてあります。
【SPSS】正規性を検定してt検定をする方法【10分でできる】
3群以上の検定をする流れ
3つ以上の群を比較するときは2段階を踏む必要があります。
step 1:まず全体としてどこかに差があるのか検定する
step 2:次に局所的にどことどこに差があるのか検定する (多重比較)
この2段階です。
step1がクラスカルウォリス検定やフリードマン検定を行う段階。
step2の検定を多重比較検定といいます。
注意点【データの並べ方】
SPSSで3群の比較を行う際、データに対応(試行の繰り返し)があるか、対応がないかによってデータの並べ方が違います。
この点は少し面倒な部分なのですが、重要ですのでまとめておきますね。
✓ 対応がないデータ→縦に並べます。
✓ 対応があるデータ→横に並べます。
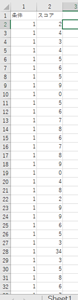
↑対応のないデータではこのように縦に並べる
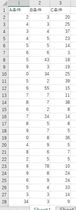
↑
データに対応がある場合はこのように横並びにします。
SPSSでクラシカルウォリス検定
ではデータを読み込んで始めていきます。
↑の写真にあるExcelファイルをリンクしておきますね。
ちなみにデータの読み込み方についてはこちらで詳しく紹介しています。
SPSSでExcelファイルやCSVファイルを読み込む方法 【まずこれを覚えましょう】
クラシカルウォリス検定は「対応のない」検定なのでデータは縦方向でした。
上のExcelファイルを読み込んでくれた場合、「対応なし」シートを選択してください。
データを読み込んだらこのように操作していきます。
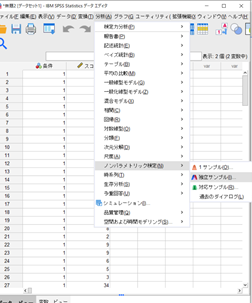
↑「分析」→「ノンパラメトリック検定」→「独立サンプル」
対応がないので「独立」しているというイメージですね。
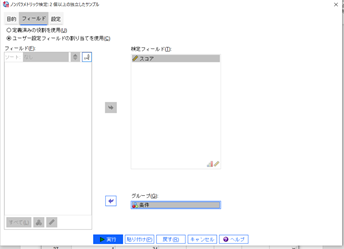
↑このような画面が出てきます。
画面左上の「フィールド」をクリックです。
「検定フィールド」に項目のデータ(今回はスコア)を、「フィールド」に「群分けする要素」(今回は条件)を投入します。
↑
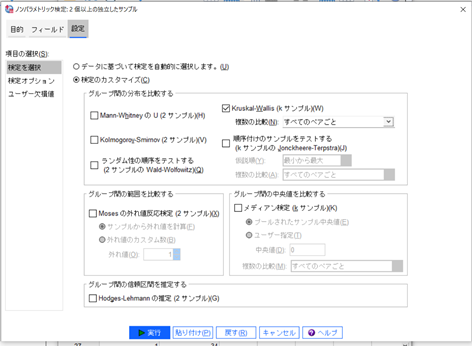
次に「設定」をクリックしてください。このような画面になります。
「検定のカスタマイズ」→「Kruskal-Walis(Kサンプル)」をクリックします。
「複数の比較」のプルダウンを「すべてのペアごと」に合わせます。
その後、「実行」を押します。
クラシカルウォリス検定の結果の見方
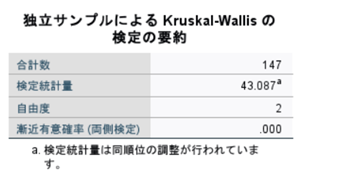
↑結果で表示される「独立サンプルによるKruskal-Walisの検定の要約」を確認します。一番下の「漸近有意確率」が0.05未満であれば「有意差あり」となります。今回は「0.000」なので有意差がありました。
ではどの群とどの群に有意差があったのでしょうか?
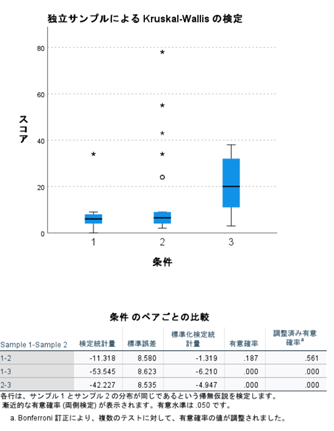
↑「条件のペアごとの比較」を見ます。このような結果も表記してくれます。便利ですね。。
上が群間の線分グラフ、下が群ごとの比較になります。多重比較の補正をBonferroni法で行っていると書いてありますね。
<結果の表記> 論文や発表資料にはこのように記載します。
Kruskal-Walis検定を行った結果、3群の間に有意差(p<0.05)が認められた。
群間の比較では、1条件と3条件の間、2条件と3条件の間にそれぞれp<0.05の有意差が認められた。
SPSSでフリードマン検定を行う
では、次に「対応のある」3群以上の検定であるフリードマン検定を行います。
フリードマン検定は「対応のある」検定ですので、データは横並びです。
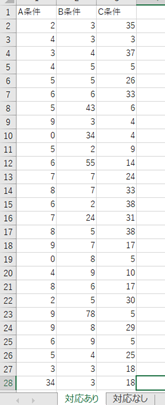
↑
デモデータでは「対応あり」シートを選択してください。

↑
データを読み込んだら「ノンパラメトリック」→「対応サンプル」を選択です。
↑
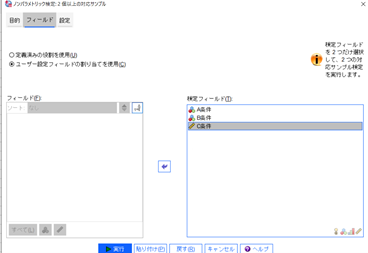
左上の画面から「フィールド」を選択し、3つの項目を「検定フィールド」へ移します。

↑
次に左上から「設定」を選択します。→「Friedman(kサンプル)」です。
「複数の比較」を選択し、「すべてのペアごと」を選択します。
フリードマン検定の結果を確認

↑
こちらがまず表示されます。「漸近有意確率」を確認します。0.05未満であれば有意差ありです。
この場合「0.000」で有意差ありなので次に「ペアごとの比較」に進みます。
↑
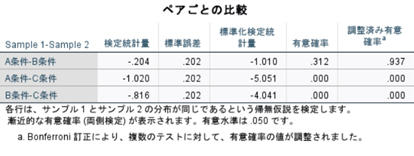
こちらを確認します。
多重比較の補正はBonferroni法によって補正されています。
この場合「A条件―C条件」、「B条件―C条件」に0.05未満の有意差が見られることがわかります。
本日は以上となります。
記事通りに進めていくことで、3群以上の比較が出来たと思います。
これからも有益な記事を書いていきます。
よろしくお願いします。


